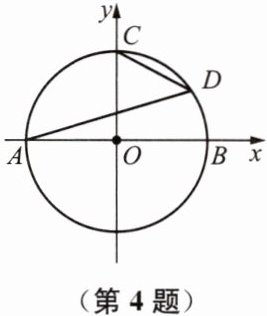
4. 如图,以原点O为圆心的圆交x轴于A、B两点,交y轴的正半轴于点C,D为第一象限内⊙O上的一点,若∠DAB= 20°,则∠OCD= ______.

65°
答案:65°
解析:
连接OD。
∵∠DAB=20°,
∴∠DOB=2∠DAB=40°。
∵A、B为圆与x轴交点,C为圆与y轴正半轴交点,
∴OA=OB=OC=OD,∠AOC=∠BOC=90°。
∴∠COD=∠COB - ∠DOB=90° - 40°=50°。
∵OC=OD,
∴∠OCD=∠ODC=(180° - ∠COD)/2=(180° - 50°)/2=65°。
65°
∵∠DAB=20°,
∴∠DOB=2∠DAB=40°。
∵A、B为圆与x轴交点,C为圆与y轴正半轴交点,
∴OA=OB=OC=OD,∠AOC=∠BOC=90°。
∴∠COD=∠COB - ∠DOB=90° - 40°=50°。
∵OC=OD,
∴∠OCD=∠ODC=(180° - ∠COD)/2=(180° - 50°)/2=65°。
65°
5. 如图,AB= AC,∠ABC= 50°,则∠D= ______.


80°
答案:80°
6. 若一条弦所对的圆心角是60°,则它所对的圆周角是
30°或150°
.答案:30°或150°.
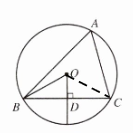
7. 如图,OD⊥BC,垂足为D,∠BOD= 62°.求∠A的度数.


答案:
解:连接OC
∵OB=OC∴△OBC是等腰三角形
∵OD⊥BC
∴OD平分∠BOC
∵∠BOD=62°
∴∠BOC=2∠BOD=124°
∴$∠A=\frac {1}{2}∠BOC=62°$
解:连接OC
∵OB=OC∴△OBC是等腰三角形
∵OD⊥BC
∴OD平分∠BOC
∵∠BOD=62°
∴∠BOC=2∠BOD=124°
∴$∠A=\frac {1}{2}∠BOC=62°$

解析:
连接OC。
∵OD⊥BC,
∴OD垂直平分BC,
∴∠BOC=2∠BOD=2×62°=124°。
∵∠A是弧BC所对的圆周角,∠BOC是弧BC所对的圆心角,
∴∠A=1/2∠BOC=1/2×124°=62°。
∠A的度数为$62^\circ$。
∵OD⊥BC,
∴OD垂直平分BC,
∴∠BOC=2∠BOD=2×62°=124°。
∵∠A是弧BC所对的圆周角,∠BOC是弧BC所对的圆心角,
∴∠A=1/2∠BOC=1/2×124°=62°。
∠A的度数为$62^\circ$。
8. 如图,△ABC内接于⊙O,且∠ABC= ∠C,点D在$\overset{\frown}{BC}$上运动,过点D作DE//BC,交AB延长线于点E,连接AD、BD.
求证:∠ADB= ∠E.

求证:∠ADB= ∠E.

答案:证明:∵DE//BC
∴∠ABC=∠E
∵∠ABC=∠C
∴∠E=∠C
∵∠C=∠ADB
∴∠ADB=∠E
∴∠ABC=∠E
∵∠ABC=∠C
∴∠E=∠C
∵∠C=∠ADB
∴∠ADB=∠E
9. 如图,四边形ABCD内接于⊙O,点E在对角线AC上,BC= DC= EC.
(1)求证:BE平分∠ABD;
(2)若∠CBD= 38°,求∠BAD的度数.

(1)求证:BE平分∠ABD;
(2)若∠CBD= 38°,求∠BAD的度数.

答案:证明:(1)因为BC=DC
所以∠CBD=∠CDB因为∠CDB=∠BAC
所以∠CBD=∠BAC
因为EC=BC
所以∠CBE=∠CEB
因为∠CEB=∠BAC+∠ABE
∠CBE=∠CBD+∠DBE
所以∠ABE=∠DBE
所以BE平分∠ABD.
(2)因为∠CBD=38°,∠CBD=∠BAC,∠CBD=∠CAD
所以∠BAD=∠BAC+∠CAD=2∠CBD=2×38°=76°.
所以∠CBD=∠CDB因为∠CDB=∠BAC
所以∠CBD=∠BAC
因为EC=BC
所以∠CBE=∠CEB
因为∠CEB=∠BAC+∠ABE
∠CBE=∠CBD+∠DBE
所以∠ABE=∠DBE
所以BE平分∠ABD.
(2)因为∠CBD=38°,∠CBD=∠BAC,∠CBD=∠CAD
所以∠BAD=∠BAC+∠CAD=2∠CBD=2×38°=76°.