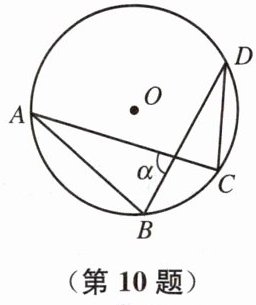
10. 如图,⊙O的半径为1 cm,弦AB、CD的长度分别为$\sqrt{2}$ cm、1 cm,求弦AC、BD所夹的锐角α.

答案:
解:连接OA,$OB\text{,}OC\text{,}OD,$BC.
∵$OA=OB=1\,\,\text{cm,}AB=\sqrt{2}\,\,\text{cm}$
∴△OAB为等腰直角三角形
∴∠AOB=90°∴$∠ACB=\frac{1}{2}∠AOB=45°$
∵$OC=OD=1\,\,\text{cm,}CD=1\,\,\text{cm}$
∴△OCD为等边三角形
∴∠COD=60°
∴$∠CBD=\frac{1}{2}∠COD=30°$
∴$\alpha =∠ACB+∠CBD=45°+30°=75°$
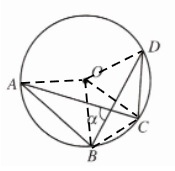
解:连接OA,$OB\text{,}OC\text{,}OD,$BC.
∵$OA=OB=1\,\,\text{cm,}AB=\sqrt{2}\,\,\text{cm}$
∴△OAB为等腰直角三角形
∴∠AOB=90°∴$∠ACB=\frac{1}{2}∠AOB=45°$
∵$OC=OD=1\,\,\text{cm,}CD=1\,\,\text{cm}$
∴△OCD为等边三角形
∴∠COD=60°
∴$∠CBD=\frac{1}{2}∠COD=30°$
∴$\alpha =∠ACB+∠CBD=45°+30°=75°$

解析:
连接OA、OB、OC、OD。
∵⊙O半径为1 cm,AB=$\sqrt{2}$ cm,
∴OA=OB=1 cm,
在△OAB中,OA²+OB²=1+1=2=AB²,
∴∠AOB=90°。
∵CD=1 cm,OC=OD=1 cm,
∴△OCD为等边三角形,∠COD=60°。
∵∠CAD=$\frac{1}{2}$∠COD=30°,∠ADB=$\frac{1}{2}$∠AOB=45°,
∴α=∠CAD+∠ADB=30°+45°=75°。
75°
∵⊙O半径为1 cm,AB=$\sqrt{2}$ cm,
∴OA=OB=1 cm,
在△OAB中,OA²+OB²=1+1=2=AB²,
∴∠AOB=90°。
∵CD=1 cm,OC=OD=1 cm,
∴△OCD为等边三角形,∠COD=60°。
∵∠CAD=$\frac{1}{2}$∠COD=30°,∠ADB=$\frac{1}{2}$∠AOB=45°,
∴α=∠CAD+∠ADB=30°+45°=75°。
75°
11. (1)如图①,在△ABC中,AB= AC,∠BAC= 90°,D是△ABC外一点,且AD= AC.若以点A为圆心,AB为半径作⊙A,则点C、D必在⊙A上,∠BAC是⊙A的圆心角,而∠BDC是圆周角,从而可得∠BDC=
(2)如图②,在四边形ABCD中,∠BAD= ∠BCD= 90°,∠BDC= 25°,求∠BAC的度数.
(3)如图③,在△ABC中,∠BAC= 45°,AD是BC边上的高,且BD= 4,CD= 2,求AD的长.
45°
.(2)如图②,在四边形ABCD中,∠BAD= ∠BCD= 90°,∠BDC= 25°,求∠BAC的度数.
解:因为∠BAD=∠BCD = 90°,所以A,B,C,D四点共圆(四边形对角互补,四点共圆)。由圆周角定理可知,∠BAC与∠BDC所对的弧都是$\overset{\frown}{BC}$。所以∠BAC=∠BDC(同弧所对的圆周角相等)。已知∠BDC = 25°,所以∠BAC = 25°。
(3)如图③,在△ABC中,∠BAC= 45°,AD是BC边上的高,且BD= 4,CD= 2,求AD的长.
$3+\sqrt {17}$
答案:1. (1)
根据圆周角定理:一条弧所对的圆周角等于它所对圆心角的一半。
已知$\angle BAC = 90^{\circ}$是圆心角,$\angle BDC$是圆周角,且$\angle BDC$与$\angle BAC$所对的弧都是$\overset{\frown}{BC}$。
所以$\angle BDC=\frac{1}{2}\angle BAC$,因为$\angle BAC = 90^{\circ}$,则$\angle BDC = 45^{\circ}$。
2. (2)
解:因为$\angle BAD=\angle BCD = 90^{\circ}$,所以$A$,$B$,$C$,$D$四点共圆(四边形对角互补,四点共圆)。
由圆周角定理可知,$\angle BAC$与$\angle BDC$所对的弧都是$\overset{\frown}{BC}$。
所以$\angle BAC=\angle BDC$(同弧所对的圆周角相等)。
已知$\angle BDC = 25^{\circ}$,所以$\angle BAC = 25^{\circ}$。
3. (3)$3+\sqrt {17}$。
根据圆周角定理:一条弧所对的圆周角等于它所对圆心角的一半。
已知$\angle BAC = 90^{\circ}$是圆心角,$\angle BDC$是圆周角,且$\angle BDC$与$\angle BAC$所对的弧都是$\overset{\frown}{BC}$。
所以$\angle BDC=\frac{1}{2}\angle BAC$,因为$\angle BAC = 90^{\circ}$,则$\angle BDC = 45^{\circ}$。
2. (2)
解:因为$\angle BAD=\angle BCD = 90^{\circ}$,所以$A$,$B$,$C$,$D$四点共圆(四边形对角互补,四点共圆)。
由圆周角定理可知,$\angle BAC$与$\angle BDC$所对的弧都是$\overset{\frown}{BC}$。
所以$\angle BAC=\angle BDC$(同弧所对的圆周角相等)。
已知$\angle BDC = 25^{\circ}$,所以$\angle BAC = 25^{\circ}$。
3. (3)$3+\sqrt {17}$。