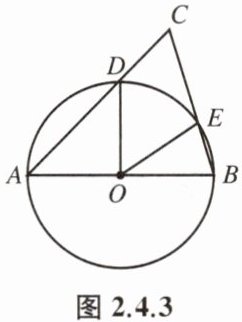
例 1 如图 2.4.3,AB 为$\odot O$的直径,C 是$\odot O$外一点,BC 交$\odot O$于点 E,AC交$\odot O$于点 D,$∠DOE= 60^{\circ }$.求$∠C$的度数.

答案:
解:连接AE,
∵∠DOE=60°
∴$∠DAE=\frac {1}{2}∠DOE=30°$
∵AB为$\odot O$的直径
∴∠AEB=90°
∴∠AEC=90°
∴∠C=180°-∠AEC-∠DAE=180°-90°-30°=60°
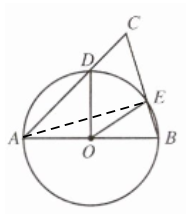
解:连接AE,
∵∠DOE=60°
∴$∠DAE=\frac {1}{2}∠DOE=30°$
∵AB为$\odot O$的直径
∴∠AEB=90°
∴∠AEC=90°
∴∠C=180°-∠AEC-∠DAE=180°-90°-30°=60°

解析:
解:连接AD、BE。
∵OA=OD=OE=OB,
∴∠OAD=∠ODA,∠OBE=∠OEB。
设∠OAD=∠ODA=α,∠OBE=∠OEB=β。
则∠AOD=180°-2α,∠BOE=180°-2β。
∵∠DOE=60°,且∠AOD+∠DOE+∠BOE=180°,
∴(180°-2α)+60°+(180°-2β)=180°,
化简得α+β=120°。
在△ABC中,∠C=180°-(∠CAD+∠CBE)=180°-(α+β)=60°。
60°
∵OA=OD=OE=OB,
∴∠OAD=∠ODA,∠OBE=∠OEB。
设∠OAD=∠ODA=α,∠OBE=∠OEB=β。
则∠AOD=180°-2α,∠BOE=180°-2β。
∵∠DOE=60°,且∠AOD+∠DOE+∠BOE=180°,
∴(180°-2α)+60°+(180°-2β)=180°,
化简得α+β=120°。
在△ABC中,∠C=180°-(∠CAD+∠CBE)=180°-(α+β)=60°。
60°
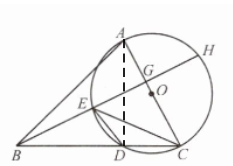
例 2 如图 2.4.4,在$\triangle ABC$中,以边 AC 为直径的$\odot O$交 BC 于点 D,在劣弧AD 上取一点 E 使$∠EBC= ∠DEC$,延长 BE 分别交 AC 于点 G,交$\odot O$于点 H.求证:$AC⊥BH.$


答案:
证明:连接AD,
∵AC为$\odot O$直径
∴∠ADC=90°
∴∠DAC+ACD=90°
∵∠EBC=∠DEC=∠DAC
∴∠EBC+ACD=90°
∴∠BGC=180°-( ∠EBC+∠ACD ) =90°
∴AC⊥BH
证明:连接AD,
∵AC为$\odot O$直径
∴∠ADC=90°
∴∠DAC+ACD=90°
∵∠EBC=∠DEC=∠DAC
∴∠EBC+ACD=90°
∴∠BGC=180°-( ∠EBC+∠ACD ) =90°
∴AC⊥BH
