1. 如图,点 A、B、C、D 都在$\odot O$上,$∠ABC= 90^{\circ },AD= 3,CD= 2$,则$\odot O$的直径为
$\sqrt{13}$
.答案:$\sqrt{13}$
解析:
∵点A、B、C、D都在$\odot O$上,$\angle ABC=90^\circ$,
∴AC是$\odot O$的直径,$\angle ADC=90^\circ$。
∵AD=3,CD=2,
∴在$Rt\triangle ADC$中,$AC=\sqrt{AD^2 + CD^2}=\sqrt{3^2 + 2^2}=\sqrt{13}$。
$\sqrt{13}$
2. 如图,已知$\odot O是\triangle ABD$的外接圆,AB 是$\odot O$的直径,CD 是$\odot O$的弦,$∠ABD= 58^{\circ }$,则$∠BCD= $
32°
.答案:32°
解析:
连接AD,
∵AB是$\odot O$的直径,
∴$\angle ADB=90^{\circ}$,
∵$\angle ABD=58^{\circ}$,
∴$\angle BAD=90^{\circ}-\angle ABD=32^{\circ}$,
∵$\angle BCD=\angle BAD$,
∴$\angle BCD=32^{\circ}$。
∵AB是$\odot O$的直径,
∴$\angle ADB=90^{\circ}$,
∵$\angle ABD=58^{\circ}$,
∴$\angle BAD=90^{\circ}-\angle ABD=32^{\circ}$,
∵$\angle BCD=\angle BAD$,
∴$\angle BCD=32^{\circ}$。
3. 如图,AB 是半圆的直径,D 是$\widehat {AC}$的中点,$∠B= 40^{\circ }$,则$∠A= $
70
°.答案:70
解析:
连接BC。
∵AB是半圆的直径,
∴∠ACB=90°。
∵∠B=40°,
∴∠A=180°-∠ACB-∠B=180°-90°-40°=50°。
70
∵AB是半圆的直径,
∴∠ACB=90°。
∵∠B=40°,
∴∠A=180°-∠ACB-∠B=180°-90°-40°=50°。
70
4. 如图,$\triangle ADC$的外接圆直径 AB 交 CD 于点 E,已知$∠C= 65^{\circ },∠D= 47^{\circ }$.求$∠CEB$的度数.
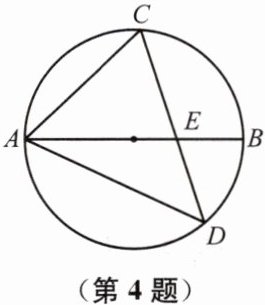

答案:
解:连接BC,
∵AB为直径
∴∠ACB=90°
∵∠ACD=65°
∴∠ECB=90°-65°=25°
∵∠B=∠D=47°
∴∠CEB=180°-∠ECB-∠B=180°-25°-47°=108°
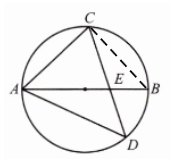
解:连接BC,
∵AB为直径
∴∠ACB=90°
∵∠ACD=65°
∴∠ECB=90°-65°=25°
∵∠B=∠D=47°
∴∠CEB=180°-∠ECB-∠B=180°-25°-47°=108°

5. 如图,在$\triangle ABC$中,$AB= AC$,以 AB 为直径的$\odot O$分别交 BC、AC 于点 D、E,$\widehat {BD}的度数是40^{\circ }$.求$∠BAC$的度数.


答案:
解:连接AD,
∵AB=AC
∴△ABC为等腰三角形.
∵AB为直径
∴∠ADB=90°,即AD⊥BC
∴D为BC中点∵O为AB中点
∴OD为△ABC的中位线
∴OD//AC∴∠BAC=∠BOD
∵$\overset{\LARGE{ \frown}}{BD}$的度数是40°,
即∠BOD=40°
∴∠BAC=40°
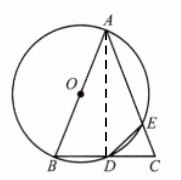
解:连接AD,
∵AB=AC
∴△ABC为等腰三角形.
∵AB为直径
∴∠ADB=90°,即AD⊥BC
∴D为BC中点∵O为AB中点
∴OD为△ABC的中位线
∴OD//AC∴∠BAC=∠BOD
∵$\overset{\LARGE{ \frown}}{BD}$的度数是40°,
即∠BOD=40°
∴∠BAC=40°

解析:
连接AD。
∵AB是⊙O的直径,
∴∠ADB=90°。
∵$\widehat{BD}$的度数是40°,
∴∠BAD=$\frac{1}{2}$×40°=20°。
在Rt△ABD中,∠ABD=90°-∠BAD=70°。
∵AB=AC,
∴∠ABC=∠ACB=70°。
∴∠BAC=180°-2×70°=40°。
∵AB是⊙O的直径,
∴∠ADB=90°。
∵$\widehat{BD}$的度数是40°,
∴∠BAD=$\frac{1}{2}$×40°=20°。
在Rt△ABD中,∠ABD=90°-∠BAD=70°。
∵AB=AC,
∴∠ABC=∠ACB=70°。
∴∠BAC=180°-2×70°=40°。