2. 设⊙O 半径为 3,点 O 到直线 l 的距离为 d,若直线 l 与⊙O 至少有一个公共点,则 d 应满足的条件是 (
A.d= 3
B.d≤3
C.d<3
D.d≥3
B
)A.d= 3
B.d≤3
C.d<3
D.d≥3
答案:B
解析:
直线与圆有公共点时,直线与圆相交或相切。
当直线与圆相切时,$d = r$,此时有一个公共点;
当直线与圆相交时,$d < r$,此时有两个公共点。
已知圆$⊙O$半径$r = 3$,点$O$到直线$l$的距离为$d$,若直线$l$与$⊙O$至少有一个公共点,则$d \leq 3$。
B
当直线与圆相切时,$d = r$,此时有一个公共点;
当直线与圆相交时,$d < r$,此时有两个公共点。
已知圆$⊙O$半径$r = 3$,点$O$到直线$l$的距离为$d$,若直线$l$与$⊙O$至少有一个公共点,则$d \leq 3$。
B
3. 在平面直角坐标系中,以点(2,3)为圆心,2 为半径的圆必定 (
A.与 x 轴相离,与 y 轴相切
B.与 x 轴、y 轴都相离
C.与 x 轴相切,与 y 轴相离
D.与 x 轴、y 轴都相切
A
)A.与 x 轴相离,与 y 轴相切
B.与 x 轴、y 轴都相离
C.与 x 轴相切,与 y 轴相离
D.与 x 轴、y 轴都相切
答案:A
解析:
圆心坐标为$(2,3)$,半径$r = 2$。
圆心到$x$轴的距离为$d_x=3$,到$y$轴的距离为$d_y=2$。
因为$d_x=3>r=2$,所以圆与$x$轴相离;
因为$d_y=2=r=2$,所以圆与$y$轴相切。
A
圆心到$x$轴的距离为$d_x=3$,到$y$轴的距离为$d_y=2$。
因为$d_x=3>r=2$,所以圆与$x$轴相离;
因为$d_y=2=r=2$,所以圆与$y$轴相切。
A
4. 已知⊙O 的半径为 5 cm,点 O 到直线 l 的距离为 d. 当 d= 4 cm 时,直线 l 与⊙O
相交
;当 d=5
cm 时,直线 l 与⊙O 相切;当 d= 6 cm 时,直线 l 与⊙O相离
.答案:相交
5
相离
5
相离
5. 直线 l 与半径为 r 的⊙O 相交,且点 O 到直线 l 的距离为 5,则 r 的取值范围是
r>5
.答案:r>5
6. ⊙O 的半径 r= 4 cm,弦 AB= 4√3 cm,以点 O 为圆心,2 cm 为半径再画一个小圆,这个小圆和 AB 的位置关系是
相切
.答案:相切
解析:
过点$O$作$OC \perp AB$于点$C$,则$AC = \frac{1}{2}AB = \frac{1}{2} × 4\sqrt{3} = 2\sqrt{3}\ cm$。
在$Rt\triangle AOC$中,$OA = r = 4\ cm$,由勾股定理得:$OC = \sqrt{OA^2 - AC^2} = \sqrt{4^2 - (2\sqrt{3})^2} = \sqrt{16 - 12} = \sqrt{4} = 2\ cm$。
因为小圆半径为$2\ cm$,圆心$O$到$AB$的距离$OC = 2\ cm$,所以小圆和$AB$的位置关系是相切。
相切
在$Rt\triangle AOC$中,$OA = r = 4\ cm$,由勾股定理得:$OC = \sqrt{OA^2 - AC^2} = \sqrt{4^2 - (2\sqrt{3})^2} = \sqrt{16 - 12} = \sqrt{4} = 2\ cm$。
因为小圆半径为$2\ cm$,圆心$O$到$AB$的距离$OC = 2\ cm$,所以小圆和$AB$的位置关系是相切。
相切
7. 如图,在 Rt△ABC 中,∠C= 90°,AC= 8,BC= 6,CD⊥AB,垂足为 D.
(1) 若以 CD 为直径画⊙O,则 AC 与⊙O 的位置关系是
(2) 若以点 C 为圆心画⊙C 与 AB 相切,则⊙C 的半径为
(3) 若以点 C 为圆心,r 为半径的圆与边 AB 有两个公共点,则 r 的取值范围是
(1) 若以 CD 为直径画⊙O,则 AC 与⊙O 的位置关系是
相交
,AB 与⊙O 有1
个公共点;(2) 若以点 C 为圆心画⊙C 与 AB 相切,则⊙C 的半径为
4.8
;(3) 若以点 C 为圆心,r 为半径的圆与边 AB 有两个公共点,则 r 的取值范围是
4.8<r≤6
.答案:相交
1
4.8
4.8<r≤6.
1
4.8
4.8<r≤6.
8. 如图,∠MON= 60°,P 为射线 OM 上的一点,且 OP= 4,以点 P 为圆心,r 为半径作⊙P.
(1) 当 r 为何值时,⊙P 分别与直线 ON 相交、相切、相离?
(2) 当 r 满足什么条件时,⊙P 与射线 ON 没有公共点?有一个公共点?有两个公共点?
(1) 当 r 为何值时,⊙P 分别与直线 ON 相交、相切、相离?
(2) 当 r 满足什么条件时,⊙P 与射线 ON 没有公共点?有一个公共点?有两个公共点?

答案:
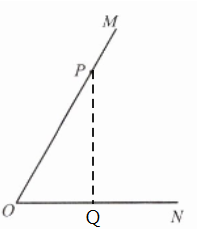
解:( 1 ) 作PQ⊥ON,垂足为点Q
∵PQ⊥ON∴∠PQO=90°
∵∠MON=60°∴∠OPQ=30°
在Rt△OPQ 中,∵OP=4,∠OPQ=30°
∴$OQ=\frac {1}{2}OP=2$∴$PQ=\sqrt{OP^2-OQ^2}=2\sqrt{3}$
∴当$r\gt 2\sqrt{3}$时,$\odot P$与直线ON相交.
当$r=2\sqrt{3}$时,$\odot P$与直线ON相切.
当$0<r<2\sqrt{3}$时,$\odot P$与直线ON相离.
( 2 ) 当$0<r<2\sqrt{3}$时,$\odot P$与射线ON没有公共点.
当$r=2\sqrt{3}$或$r\gt 4$时,$\odot P$与射线ON有一个公共点.
当$2\sqrt{3}<r≤4$时,$\odot P$与射线ON有两个公共点.
解:( 1 ) 作PQ⊥ON,垂足为点Q
∵PQ⊥ON∴∠PQO=90°
∵∠MON=60°∴∠OPQ=30°
在Rt△OPQ 中,∵OP=4,∠OPQ=30°
∴$OQ=\frac {1}{2}OP=2$∴$PQ=\sqrt{OP^2-OQ^2}=2\sqrt{3}$
∴当$r\gt 2\sqrt{3}$时,$\odot P$与直线ON相交.
当$r=2\sqrt{3}$时,$\odot P$与直线ON相切.
当$0<r<2\sqrt{3}$时,$\odot P$与直线ON相离.
( 2 ) 当$0<r<2\sqrt{3}$时,$\odot P$与射线ON没有公共点.
当$r=2\sqrt{3}$或$r\gt 4$时,$\odot P$与射线ON有一个公共点.
当$2\sqrt{3}<r≤4$时,$\odot P$与射线ON有两个公共点.

解析:
(1)过点 P 作 PH⊥ON 于点 H,在 Rt△POH 中,∠MON=60°,OP=4,PH=OP·sin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$。当 r>2$\sqrt{3}$时,⊙P 与直线 ON 相交;当 r=2$\sqrt{3}$时,⊙P 与直线 ON 相切;当 0<r<2$\sqrt{3}$时,⊙P 与直线 ON 相离。
(2)当 0<r<2$\sqrt{3}$时,⊙P 与射线 ON 没有公共点;当 r=2$\sqrt{3}$或 r>4 时,⊙P 与射线 ON 有一个公共点;当 2$\sqrt{3}$<r≤4 时,⊙P 与射线 ON 有两个公共点。
(2)当 0<r<2$\sqrt{3}$时,⊙P 与射线 ON 没有公共点;当 r=2$\sqrt{3}$或 r>4 时,⊙P 与射线 ON 有一个公共点;当 2$\sqrt{3}$<r≤4 时,⊙P 与射线 ON 有两个公共点。