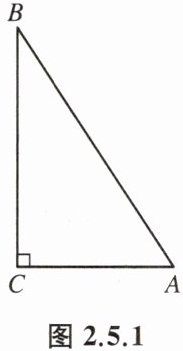
例 如图 2.5.1,在 Rt△ABC 中,AB= 6 cm,AC= 3 cm.
(1) 圆心为点 C,半径分别为 2 cm、4 cm 的两个圆与直线 AB 有怎样的位置关系?
(2) 半径 r 多长时,直线 AB 与⊙C 相切?
(3) 若⊙C 与边 AB 有一个公共点,则半径 r 应取怎样的值?
(1) 圆心为点 C,半径分别为 2 cm、4 cm 的两个圆与直线 AB 有怎样的位置关系?
(2) 半径 r 多长时,直线 AB 与⊙C 相切?
(3) 若⊙C 与边 AB 有一个公共点,则半径 r 应取怎样的值?

答案:
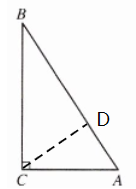
解:$\left( 1 \right) $作CD⊥AB,垂足为点D\
在Rt△ABC中, ∵$AB=6\,\,\text{cm,}AC=3\,\,\text{cm}\ $
∴$BC=\sqrt{AB^2-AC^2}=3\sqrt{3}\,\,\text{cm}\ $
∵点C到直线AB的距离$CD=\frac{3×3\sqrt{3}}{6}=\frac{3\sqrt{3}}{2}\,\,\text{cm}\ $
∵$2\ \text{cm}\lt \frac{3\sqrt{3}}{2}\,\,\text{cm}\lt 4\,\,\text{cm}\ $
∴半径为$2\,\,\text{cm}$的圆与直线AB相离,半径为$4\,\,\text{cm}$的圆与直线AB相交.\
$\left( 2 \right) $∵圆心C到直线AB的距离为$\frac{3\sqrt{3}}{2}\,\,\text{cm}\ $
∴当半径$\ r=\frac{3\sqrt{3}}{2}\,\,\text{cm}$时,直线AB与$\odot C$相切.\
$\left( 3 \right) $∵$AC=3\,\,\text{cm},$$BC=3\sqrt{3}\,\,\text{cm,}\odot C$与边AB有一个公共交点\
∴$3\,\,\text{cm}<r≤3\sqrt{3}cm$或$r=\frac{3\sqrt{3}}{2}cm.$
解:$\left( 1 \right) $作CD⊥AB,垂足为点D\
在Rt△ABC中, ∵$AB=6\,\,\text{cm,}AC=3\,\,\text{cm}\ $
∴$BC=\sqrt{AB^2-AC^2}=3\sqrt{3}\,\,\text{cm}\ $
∵点C到直线AB的距离$CD=\frac{3×3\sqrt{3}}{6}=\frac{3\sqrt{3}}{2}\,\,\text{cm}\ $
∵$2\ \text{cm}\lt \frac{3\sqrt{3}}{2}\,\,\text{cm}\lt 4\,\,\text{cm}\ $
∴半径为$2\,\,\text{cm}$的圆与直线AB相离,半径为$4\,\,\text{cm}$的圆与直线AB相交.\
$\left( 2 \right) $∵圆心C到直线AB的距离为$\frac{3\sqrt{3}}{2}\,\,\text{cm}\ $
∴当半径$\ r=\frac{3\sqrt{3}}{2}\,\,\text{cm}$时,直线AB与$\odot C$相切.\
$\left( 3 \right) $∵$AC=3\,\,\text{cm},$$BC=3\sqrt{3}\,\,\text{cm,}\odot C$与边AB有一个公共交点\
∴$3\,\,\text{cm}<r≤3\sqrt{3}cm$或$r=\frac{3\sqrt{3}}{2}cm.$

1. 已知⊙O 的半径为 5 cm,点 O 到直线 l 的距离为 5 cm,则直线 l 与⊙O 的位置关系是 (
A.相交
B.相切
C.相离
D.无法确定
B
)A.相交
B.相切
C.相离
D.无法确定
答案:B