6. 如图,点 A、B、C、D、E 在⊙O 上,且$\widehat{AB}$的度数为 50°,则∠E +∠C= ______
155°
.答案:155°
解析:
连接AE。
∵$\widehat{AB}$的度数为50°,
∴∠AEB=$\frac{1}{2}$×50°=25°。
∵四边形ACDE内接于⊙O,
∴∠C+∠AED=180°。
∵∠AED=∠AEB+∠E,
∴∠C+∠AEB+∠E=180°,
∴∠C+∠E=180°-∠AEB=180°-25°=155°。
155°
∵$\widehat{AB}$的度数为50°,
∴∠AEB=$\frac{1}{2}$×50°=25°。
∵四边形ACDE内接于⊙O,
∴∠C+∠AED=180°。
∵∠AED=∠AEB+∠E,
∴∠C+∠AEB+∠E=180°,
∴∠C+∠E=180°-∠AEB=180°-25°=155°。
155°
7. 如图,⊙O 的内接四边形 ABCD 两组对边的延长线分别交于点 E、F,若∠E= 42°,∠F= 38°,则∠A=
50°
.答案:50°
解析:
在△ABE和△ADF中,∠E=42°,∠F=38°,设∠A=x。
因为∠ADC是△ADF的外角,所以∠ADC=∠A+∠F=x+38°。
因为∠ABC是△ABE的外角,所以∠ABC=∠A+∠E=x+42°。
由于四边形ABCD是⊙O的内接四边形,所以∠ADC+∠ABC=180°。
即(x+38°)+(x+42°)=180°,
2x+80°=180°,
2x=100°,
x=50°。
50°
因为∠ADC是△ADF的外角,所以∠ADC=∠A+∠F=x+38°。
因为∠ABC是△ABE的外角,所以∠ABC=∠A+∠E=x+42°。
由于四边形ABCD是⊙O的内接四边形,所以∠ADC+∠ABC=180°。
即(x+38°)+(x+42°)=180°,
2x+80°=180°,
2x=100°,
x=50°。
50°
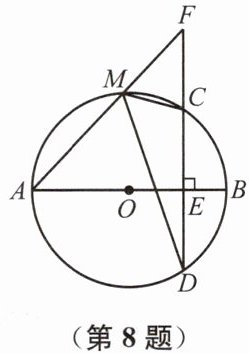
8. 已知:如图,⊙O 的直径 AB 垂直于弦 CD,垂足为 E,F 为 DC 延长线上的一点,连接 AF 交⊙O 于点 M.求证:∠AMD= ∠FMC.

答案:
证明:连接AC,BC
∵ 四边形ABCM为⊙O的内接四边形
∴ ∠AMC+∠B=180°∵ ∠AMC+∠FMC=180°
∴ ∠B=∠FMC∵ AB是直径,AB⊥CD
∴ ∠ACB=∠CEB=90°
∴ ∠B+∠BCE=∠BCE+∠ACE=90°
∴ ∠B=∠ACE
∵ ∠B=∠FMC,∠ACE=∠AMD
∴ ∠AMD=∠FMC
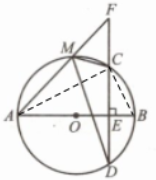
证明:连接AC,BC
∵ 四边形ABCM为⊙O的内接四边形
∴ ∠AMC+∠B=180°∵ ∠AMC+∠FMC=180°
∴ ∠B=∠FMC∵ AB是直径,AB⊥CD
∴ ∠ACB=∠CEB=90°
∴ ∠B+∠BCE=∠BCE+∠ACE=90°
∴ ∠B=∠ACE
∵ ∠B=∠FMC,∠ACE=∠AMD
∴ ∠AMD=∠FMC

9. 已知:如图,圆内接四边形 ABCD 的两组对边的延长线分别交于点 E、F,∠AEB、∠AFD 的平分线交于点 P.求证:PE⊥PF.


答案:证明:∵四边形ABCD内接于圆,
∴∠A+∠BCD=180°
∵∠BCD+∠BCF=180°
∴∠BCF=∠A,
∵FM平分∠BFC,
∴∠BFN = ∠CFN,
∵∠EMP=∠A+∠BFN, ∠PNE=∠BCF+∠CFN
∴∠EMP=∠PNE,
∴EM=EN,
∵PE平分∠MEN,
∴PE⊥PF
∴∠A+∠BCD=180°
∵∠BCD+∠BCF=180°
∴∠BCF=∠A,
∵FM平分∠BFC,
∴∠BFN = ∠CFN,
∵∠EMP=∠A+∠BFN, ∠PNE=∠BCF+∠CFN
∴∠EMP=∠PNE,
∴EM=EN,
∵PE平分∠MEN,
∴PE⊥PF