1. 在圆内接四边形 ABCD 中,∠A、∠B、∠C 的度数之比为 4∶3∶5,则∠D 等于 (
A.60°
B.90°
C.120°
D.150°
C
)A.60°
B.90°
C.120°
D.150°
答案:C
解析:
∵四边形ABCD是圆内接四边形,
∴∠A+∠C=180°,∠B+∠D=180°。
设∠A=4x,∠B=3x,∠C=5x,
则4x+5x=180°,解得x=20°。
∴∠B=3x=60°,
∴∠D=180°-∠B=120°。
C
2. 如图,两圆相交于 A、B 两点,小圆经过大圆的圆心 O,点 C、D 分别在两圆上,若∠ADB= 100°,则∠ACB 的度数为 (
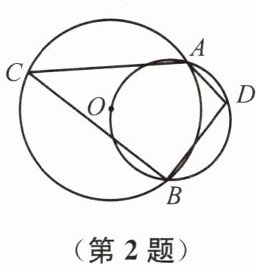
A.35°
B.40°
C.50°
D.80°
B
)
A.35°
B.40°
C.50°
D.80°
答案:B
3. 如图,四边形 ABCD 是半圆的内接四边形,AB 是直径,$\widehat{DC}= \widehat{CB}$.若∠C= 110°,则∠ABC 的度数为 (
A.55°
B.60°
C.65°
D.70°
A
)A.55°
B.60°
C.65°
D.70°
答案:A
解析:
连接AC。
∵四边形ABCD是半圆内接四边形,
∴∠DAB+∠C=180°,
∵∠C=110°,
∴∠DAB=180°-110°=70°。
∵$\widehat{DC}=\widehat{CB}$,
∴∠CAB=∠CAD=$\frac{1}{2}$∠DAB=35°。
∵AB是直径,
∴∠ACB=90°,
∴∠ABC=90°-∠CAB=90°-35°=55°。
A
∵四边形ABCD是半圆内接四边形,
∴∠DAB+∠C=180°,
∵∠C=110°,
∴∠DAB=180°-110°=70°。
∵$\widehat{DC}=\widehat{CB}$,
∴∠CAB=∠CAD=$\frac{1}{2}$∠DAB=35°。
∵AB是直径,
∴∠ACB=90°,
∴∠ABC=90°-∠CAB=90°-35°=55°。
A
4. 如图,四边形 ABCD 内接于⊙O,∠BOD= 100°,则∠BCD=
130
°.答案:130
解析:
∵∠BOD=100°,
∴∠BAD=$\frac{1}{2}$∠BOD=50°,
∵四边形ABCD内接于⊙O,
∴∠BAD+∠BCD=180°,
∴∠BCD=180°-∠BAD=130°。
130
5. 如图,已知 AB 是半圆 O 的直径,∠BAC= 32°,D 是$\widehat{AC}$上一点,则∠D 的度数是
122°
.答案:122°
解析:
∵AB是半圆O的直径,
∴∠ACB=90°,
∵∠BAC=32°,
∴∠B=90°-∠BAC=58°,
∵四边形ABCD是圆内接四边形,
∴∠D=180°-∠B=122°.
122°