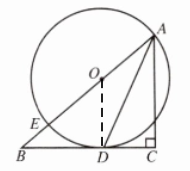
例2 如图2.5.3,在△ABC中,∠C= 90°,O是AB上一点,以OA为半径的⊙O与BC相切于点D,与AB相交于点E.
(1)求证:AD是∠BAC的平分线;
(2)若BE= 2,BD= 4,求AE的长.

(1)求证:AD是∠BAC的平分线;
(2)若BE= 2,BD= 4,求AE的长.

答案:
解:(1)连接OD
∵BC与⊙O相切于点D
∴OD⊥BD,又∠C=90°
∴AC//OD,∴∠ODA=∠DAC
又∵OA=OD,∴∠DAO=∠ODA
∴∠CAD=∠DAO
∴AD是∠BAC的平分线
(2)设OE=x,则OD=x,OB=x+2
在Rt△OBD中,OD²+BD²=OB²
即x²+4²=(x+2)²,解得x=3
则AE=2OE=6
解:(1)连接OD
∵BC与⊙O相切于点D
∴OD⊥BD,又∠C=90°
∴AC//OD,∴∠ODA=∠DAC
又∵OA=OD,∴∠DAO=∠ODA
∴∠CAD=∠DAO
∴AD是∠BAC的平分线
(2)设OE=x,则OD=x,OB=x+2
在Rt△OBD中,OD²+BD²=OB²
即x²+4²=(x+2)²,解得x=3
则AE=2OE=6

1. 给出下列说法:① 与圆只有一个公共点的直线是圆的切线;② 与圆心的距离等于半径的直线是圆的切线;③ 垂直于圆的半径的直线是圆的切线;④ 过圆的半径的外端的直线是圆的切线;⑤ 经过圆心和切点的直线垂直于这条切线.其中,正确的是
①②⑤
. (填序号)答案:①②⑤
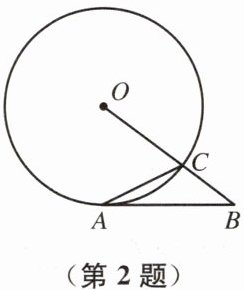
2. 如图,⊙O与AB相切于点A,BO与⊙O相交于点C,且∠BAC= 27°,则∠B= ______°.

36
答案:36
解析:
连接OA。
∵AB与⊙O相切于点A,
∴OA⊥AB,∠OAB=90°。
∵OA=OC,
∴∠OAC=∠OCA。
设∠B=x°,则∠OCA=∠BAC+∠B=27°+x°,
∴∠OAC=27°+x°。
∵∠OAB=∠OAC+∠BAC,
∴90°=27°+x°+27°,
解得x=36。
∠B=36°。
∵AB与⊙O相切于点A,
∴OA⊥AB,∠OAB=90°。
∵OA=OC,
∴∠OAC=∠OCA。
设∠B=x°,则∠OCA=∠BAC+∠B=27°+x°,
∴∠OAC=27°+x°。
∵∠OAB=∠OAC+∠BAC,
∴90°=27°+x°+27°,
解得x=36。
∠B=36°。
3. 如图,四边形ABCD内接于⊙O,AB是⊙O的直径,过点C的切线与AB的延长线交于点P,若∠P= 40°,则∠D的度数为
115°
.答案:115°
解析:
连接OC,
∵PC是⊙O的切线,
∴OC⊥PC,∠OCP=90°,
∵∠P=40°,
∴∠COP=180°-∠OCP-∠P=50°,
∵OA=OC,
∴∠OAC=∠OCA,
∵∠COP=∠OAC+∠OCA=2∠OAC,
∴∠OAC=25°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵四边形ABCD内接于⊙O,
∴∠D+∠ABC=180°,
∵∠ABC=180°-∠OAC-∠ACB=65°,
∴∠D=180°-∠ABC=115°.
115°
∵PC是⊙O的切线,
∴OC⊥PC,∠OCP=90°,
∵∠P=40°,
∴∠COP=180°-∠OCP-∠P=50°,
∵OA=OC,
∴∠OAC=∠OCA,
∵∠COP=∠OAC+∠OCA=2∠OAC,
∴∠OAC=25°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵四边形ABCD内接于⊙O,
∴∠D+∠ABC=180°,
∵∠ABC=180°-∠OAC-∠ACB=65°,
∴∠D=180°-∠ABC=115°.
115°
4. 两个同心圆的大圆半径为5 cm,小圆半径为3 cm,大圆的弦AB与小圆相切,切点为C,则弦AB的长是
8cm
.答案:8cm
解析:
连接OA,OC。
∵AB与小圆相切于点C,
∴OC⊥AB,OC=3cm。
∵OA为大圆半径,
∴OA=5cm。
在Rt△OAC中,$AC=\sqrt{OA^2-OC^2}=\sqrt{5^2-3^2}=\sqrt{25-9}=\sqrt{16}=4$cm。
∵OC⊥AB,O为圆心,
∴AB=2AC=2×4=8cm。
8 cm
∵AB与小圆相切于点C,
∴OC⊥AB,OC=3cm。
∵OA为大圆半径,
∴OA=5cm。
在Rt△OAC中,$AC=\sqrt{OA^2-OC^2}=\sqrt{5^2-3^2}=\sqrt{25-9}=\sqrt{16}=4$cm。
∵OC⊥AB,O为圆心,
∴AB=2AC=2×4=8cm。
8 cm
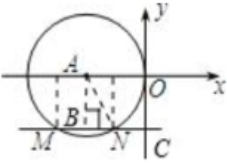
5. 如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、N两点,若点M的坐标是(-4,-2),则点N的坐标是______.


答案:
解:分别过点M、N作x轴的垂线,过点A作AB⊥MN,
连接AN,则BM=BN,
设圆A的半径为r,则AN=r, AB=2,\
BM=BN=4-r,
在Rt△ABN中,根据勾股定理,
$2^2+(4-r)^2=r^2,$可得: r=2.5,
∴ BN=4-2.5=1.5,
则N到y轴的距离为: AO-BN=2.5-1.5=1,
又点N在第三象限,
∴N的坐标为(-1, -2) .
解:分别过点M、N作x轴的垂线,过点A作AB⊥MN,
连接AN,则BM=BN,
设圆A的半径为r,则AN=r, AB=2,\
BM=BN=4-r,
在Rt△ABN中,根据勾股定理,
$2^2+(4-r)^2=r^2,$可得: r=2.5,
∴ BN=4-2.5=1.5,
则N到y轴的距离为: AO-BN=2.5-1.5=1,
又点N在第三象限,
∴N的坐标为(-1, -2) .

解析:
设⊙A的半径为$r$,因为⊙A与y轴相切于原点O,所以圆心A的坐标为$(-r,0)$。
直线MN平行于x轴,点M的坐标是$(-4,-2)$,所以点N的纵坐标为$-2$,设点N的坐标为$(x,-2)$。
圆心A$(-r,0)$到直线MN的距离为$|0 - (-2)| = 2$,MN的长度为$|x - (-4)| = |x + 4|$,根据垂径定理,圆心到弦的距离垂直平分弦,所以弦长的一半为$\frac{|x + 4|}{2}$。
由勾股定理得:$(\frac{|x + 4|}{2})^2 + 2^2 = r^2$。
又因为点M$(-4,-2)$在⊙A上,所以$(-4 + r)^2 + (-2 - 0)^2 = r^2$,即$(r - 4)^2 + 4 = r^2$,展开得$r^2 - 8r + 16 + 4 = r^2$,解得$r = \frac{5}{2}$。
将$r = \frac{5}{2}$代入$(\frac{|x + 4|}{2})^2 + 4 = (\frac{5}{2})^2$,即$(\frac{|x + 4|}{2})^2 = \frac{25}{4} - 4 = \frac{9}{4}$,所以$\frac{|x + 4|}{2} = \frac{3}{2}$,$|x + 4| = 3$,解得$x = -1$或$x = -7$(舍去),故点N的坐标是$(-1,-2)$。
$(-1,-2)$
直线MN平行于x轴,点M的坐标是$(-4,-2)$,所以点N的纵坐标为$-2$,设点N的坐标为$(x,-2)$。
圆心A$(-r,0)$到直线MN的距离为$|0 - (-2)| = 2$,MN的长度为$|x - (-4)| = |x + 4|$,根据垂径定理,圆心到弦的距离垂直平分弦,所以弦长的一半为$\frac{|x + 4|}{2}$。
由勾股定理得:$(\frac{|x + 4|}{2})^2 + 2^2 = r^2$。
又因为点M$(-4,-2)$在⊙A上,所以$(-4 + r)^2 + (-2 - 0)^2 = r^2$,即$(r - 4)^2 + 4 = r^2$,展开得$r^2 - 8r + 16 + 4 = r^2$,解得$r = \frac{5}{2}$。
将$r = \frac{5}{2}$代入$(\frac{|x + 4|}{2})^2 + 4 = (\frac{5}{2})^2$,即$(\frac{|x + 4|}{2})^2 = \frac{25}{4} - 4 = \frac{9}{4}$,所以$\frac{|x + 4|}{2} = \frac{3}{2}$,$|x + 4| = 3$,解得$x = -1$或$x = -7$(舍去),故点N的坐标是$(-1,-2)$。
$(-1,-2)$