6. 如图,AB为⊙O的直径,过圆上一点D作⊙O的切线,交BA的延长线于点C,过点O作OE//AD,交CD于点E,连接BE.直线BE与⊙O相切吗? 请说明理由.
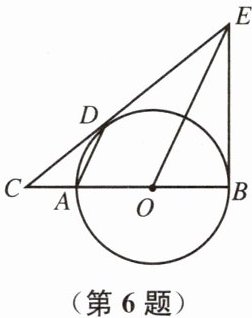

答案:
解:直线BE与⊙O相切,理由如下:
连接OD,BD
∵OE//AD,CD与⊙O相切于点D
∴OE⊥BD
∴OE平分∠BED
∵OB=OD,OD⊥CE
∴OB⊥BE
∴BE与⊙O相切
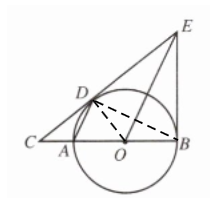
解:直线BE与⊙O相切,理由如下:
连接OD,BD
∵OE//AD,CD与⊙O相切于点D
∴OE⊥BD
∴OE平分∠BED
∵OB=OD,OD⊥CE
∴OB⊥BE
∴BE与⊙O相切

解析:
直线BE与⊙O相切,理由如下:
连接OD,
∵CD是⊙O的切线,
∴OD⊥CD,即∠ODE=90°,
∵OE//AD,
∴∠DAO=∠EOB,∠ADO=∠DOE,
∵OA=OD,
∴∠DAO=∠ADO,
∴∠EOB=∠DOE,
在△EOB和△EOD中,
$\left\{\begin{array}{l} OB=OD\\ ∠EOB=∠EOD\\ OE=OE\end{array}\right.$
∴△EOB≌△EOD(SAS),
∴∠OBE=∠ODE=90°,
∵OB是⊙O的半径,
∴直线BE与⊙O相切.
连接OD,
∵CD是⊙O的切线,
∴OD⊥CD,即∠ODE=90°,
∵OE//AD,
∴∠DAO=∠EOB,∠ADO=∠DOE,
∵OA=OD,
∴∠DAO=∠ADO,
∴∠EOB=∠DOE,
在△EOB和△EOD中,
$\left\{\begin{array}{l} OB=OD\\ ∠EOB=∠EOD\\ OE=OE\end{array}\right.$
∴△EOB≌△EOD(SAS),
∴∠OBE=∠ODE=90°,
∵OB是⊙O的半径,
∴直线BE与⊙O相切.
7. 如图,正方形ABCD边长为4,O为对角线AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点M,与AD、AB分别相交于点E、F.
(1)求证:CD与⊙O相切;
(2)求⊙O的半径.

(1)求证:CD与⊙O相切;
(2)求⊙O的半径.

答案:
解:(1)证明:过点O作OG⊥CD交CD于点G
连接OM
则OM⊥BC,四边形OMCG为矩形
∵AC是正方形ABCD的对角线
∴∠DCA=45°,∴△CGO是等腰直角三角形
∴OG=CG,∴矩形OMCG是正方形
∴OM=OG
∴CD与⊙O相切
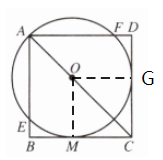
解:(2)∵正方形的边长为4

∴$AC=4\sqrt{2}$
设AO=x,则OM=x
则$OC=\sqrt{2}x$
则$AC=(1+\sqrt{2})x$
则$(1+\sqrt{2})x=4\sqrt{2}$
$x=\frac {4\sqrt{2}}{\sqrt{2}+1}$
$x=\frac {4\sqrt{2}(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}$
$x=8-4\sqrt{2}$
∴⊙O的半径为$8-4\sqrt{2}$
解:(1)证明:过点O作OG⊥CD交CD于点G
连接OM
则OM⊥BC,四边形OMCG为矩形
∵AC是正方形ABCD的对角线
∴∠DCA=45°,∴△CGO是等腰直角三角形
∴OG=CG,∴矩形OMCG是正方形
∴OM=OG
∴CD与⊙O相切

解:(2)∵正方形的边长为4

∴$AC=4\sqrt{2}$
设AO=x,则OM=x
则$OC=\sqrt{2}x$
则$AC=(1+\sqrt{2})x$
则$(1+\sqrt{2})x=4\sqrt{2}$
$x=\frac {4\sqrt{2}}{\sqrt{2}+1}$
$x=\frac {4\sqrt{2}(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}$
$x=8-4\sqrt{2}$
∴⊙O的半径为$8-4\sqrt{2}$
8. 在△ABC中,∠C= 90°,以边AB上的点O为圆心,OA为半径作圆,与BC相切于点D,分别交AB、AC于点E、F.
(1)如图①,连接AD,若∠CAD= 25°,求∠B的度数;
(2)如图②,若F为$\widehat{AD}$的中点,⊙O的半径为1,求AB的长.

(1)如图①,连接AD,若∠CAD= 25°,求∠B的度数;
(2)如图②,若F为$\widehat{AD}$的中点,⊙O的半径为1,求AB的长.

答案:
解:(1)连接OD
∵BC与圆O相切∴∠ODC=90°
∵∠C=90°∴OD//AC
∴∠ADO=∠CAD
∵OA=OD∴∠OAD=∠ADO
∴∠OAD=∠CAD
∵∠CAD=25°
∴∠CAB=∠CAD+AOD=50°
∴∠B=90°-∠CAB=40°.
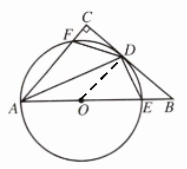
(2)连接OD,OF
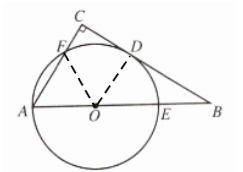
因为F是$\widehat{AD}$的中点
所以∠AOF=∠FOD
因为OD//AC
所以∠AFO=∠FOD
所以∠AFO=∠AOF
因为OA=OF
所以∠AFO=∠OAF
所以△AFO是等边三角形
所以∠CAB=60°
所以∠B=30°
因为OD=1
所以OB=2OD=2
所以AB=OA+OB=3
解:(1)连接OD
∵BC与圆O相切∴∠ODC=90°
∵∠C=90°∴OD//AC
∴∠ADO=∠CAD
∵OA=OD∴∠OAD=∠ADO
∴∠OAD=∠CAD
∵∠CAD=25°
∴∠CAB=∠CAD+AOD=50°
∴∠B=90°-∠CAB=40°.

(2)连接OD,OF

因为F是$\widehat{AD}$的中点
所以∠AOF=∠FOD
因为OD//AC
所以∠AFO=∠FOD
所以∠AFO=∠AOF
因为OA=OF
所以∠AFO=∠OAF
所以△AFO是等边三角形
所以∠CAB=60°
所以∠B=30°
因为OD=1
所以OB=2OD=2
所以AB=OA+OB=3