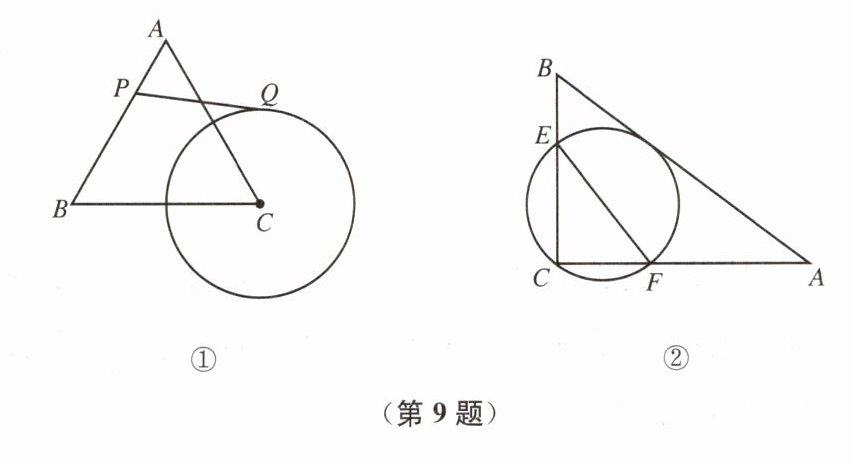
9. (1)如图①,等边三角形ABC的边长为4,⊙C的半径为2,P为边AB上一动点,过点P作⊙C的切线PQ,切点为Q,则线段PQ的最小值为
(2)如图②,在△ABC中,AB= 5,AC= 4,BC= 3,过点C且与边AB相切的圆与线段CB、CA分别相交于点E、F,则线段EF的最小值为
2√2
.(2)如图②,在△ABC中,AB= 5,AC= 4,BC= 3,过点C且与边AB相切的圆与线段CB、CA分别相交于点E、F,则线段EF的最小值为
12/5
.
答案:1. (1)
连接$CP$,$CQ$:
因为$PQ$是$\odot C$的切线,所以$CQ\perp PQ$,在$Rt\triangle CPQ$中,根据勾股定理$PQ = \sqrt{CP^{2}-CQ^{2}}$。
已知$CQ = 2$(半径),所以$PQ=\sqrt{CP^{2}-4}$。
当$CP\perp AB$时,$CP$的值最小。
因为$\triangle ABC$是等边三角形,边长$AB = 4$,根据等边三角形三线合一性质,$CP\perp AB$时,$AP = BP=\frac{1}{2}AB = 2$。
再根据勾股定理$CP=\sqrt{AC^{2}-AP^{2}}$,$AC = 4$,$AP = 2$,则$CP=\sqrt{4^{2}-2^{2}}=\sqrt{16 - 4}=\sqrt{12}=2\sqrt{3}$。
把$CP = 2\sqrt{3}$代入$PQ=\sqrt{CP^{2}-4}$,得$PQ=\sqrt{(2\sqrt{3})^{2}-4}=\sqrt{12 - 4}=\sqrt{8}=2\sqrt{2}$。
2. (2)
因为$AB = 5$,$AC = 4$,$BC = 3$,满足$BC^{2}+AC^{2}=3^{2}+4^{2}=25=AB^{2}$,所以$\angle ACB = 90^{\circ}$。
设切点为$D$,连接$CD$,设圆的半径为$r$。
根据三角形面积公式$S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}(AC + BC+AB)\cdot r$(利用三角形面积的两种表示方法,一种是$\frac{1}{2}AC\cdot BC$,另一种是$\frac{1}{2}(AC + BC + AB)\cdot r$,这里$r$是内切圆半径的推广形式),$S_{\triangle ABC}=\frac{1}{2}×3×4 = 6$,$\frac{1}{2}(3 + 4+5)\cdot r=6$,解得$r = 1$。
因为$\angle ACB = 90^{\circ}$,$EF$是圆的直径($\angle ACB = 90^{\circ}$,$EF$所对圆周角为$90^{\circ}$,所以$EF$是直径)。
当$CD$为圆的直径时$EF$最小,根据三角形面积$S_{\triangle ABC}=\frac{1}{2}AB\cdot CD=\frac{1}{2}AC\cdot BC$,则$CD=\frac{AC\cdot BC}{AB}$。
把$AC = 4$,$BC = 3$,$AB = 5$代入得$CD=\frac{3×4}{5}=\frac{12}{5}$,即$EF$的最小值为$\frac{12}{5}$。
故答案为:(1)$2\sqrt{2}$;(2)$\frac{12}{5}$。
连接$CP$,$CQ$:
因为$PQ$是$\odot C$的切线,所以$CQ\perp PQ$,在$Rt\triangle CPQ$中,根据勾股定理$PQ = \sqrt{CP^{2}-CQ^{2}}$。
已知$CQ = 2$(半径),所以$PQ=\sqrt{CP^{2}-4}$。
当$CP\perp AB$时,$CP$的值最小。
因为$\triangle ABC$是等边三角形,边长$AB = 4$,根据等边三角形三线合一性质,$CP\perp AB$时,$AP = BP=\frac{1}{2}AB = 2$。
再根据勾股定理$CP=\sqrt{AC^{2}-AP^{2}}$,$AC = 4$,$AP = 2$,则$CP=\sqrt{4^{2}-2^{2}}=\sqrt{16 - 4}=\sqrt{12}=2\sqrt{3}$。
把$CP = 2\sqrt{3}$代入$PQ=\sqrt{CP^{2}-4}$,得$PQ=\sqrt{(2\sqrt{3})^{2}-4}=\sqrt{12 - 4}=\sqrt{8}=2\sqrt{2}$。
2. (2)
因为$AB = 5$,$AC = 4$,$BC = 3$,满足$BC^{2}+AC^{2}=3^{2}+4^{2}=25=AB^{2}$,所以$\angle ACB = 90^{\circ}$。
设切点为$D$,连接$CD$,设圆的半径为$r$。
根据三角形面积公式$S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}(AC + BC+AB)\cdot r$(利用三角形面积的两种表示方法,一种是$\frac{1}{2}AC\cdot BC$,另一种是$\frac{1}{2}(AC + BC + AB)\cdot r$,这里$r$是内切圆半径的推广形式),$S_{\triangle ABC}=\frac{1}{2}×3×4 = 6$,$\frac{1}{2}(3 + 4+5)\cdot r=6$,解得$r = 1$。
因为$\angle ACB = 90^{\circ}$,$EF$是圆的直径($\angle ACB = 90^{\circ}$,$EF$所对圆周角为$90^{\circ}$,所以$EF$是直径)。
当$CD$为圆的直径时$EF$最小,根据三角形面积$S_{\triangle ABC}=\frac{1}{2}AB\cdot CD=\frac{1}{2}AC\cdot BC$,则$CD=\frac{AC\cdot BC}{AB}$。
把$AC = 4$,$BC = 3$,$AB = 5$代入得$CD=\frac{3×4}{5}=\frac{12}{5}$,即$EF$的最小值为$\frac{12}{5}$。
故答案为:(1)$2\sqrt{2}$;(2)$\frac{12}{5}$。
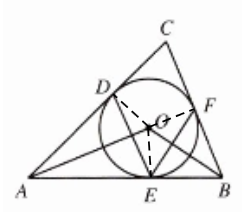
例1 如图2.5.4,在△ABC中,∠ABC= 70°,∠BAC= 50°,△ABC的内切圆O分别切AC、AB、BC于点D、E、F.求∠DEF及∠AOB的度数.


答案:
解:连接OD,OE,OF
∵ AC、AB、BC为⊙O的切线
∴ OD⊥AC,OE⊥AB,OF⊥BC
∴ ∠ODC=∠OFC=90°
∵ ∠ABC=70°,∠BAC=50
°∴ ∠C=180°-70°-50°=60°
∴ ∠DOF=360°-90°-90°-60°=120°
∴$ ∠DEF=\frac 1 2∠DOF=60°$
∵ OD=OE=OF∴ AO平分∠CAB,BO平分∠CBA
∴$ ∠OAB=\frac 12∠BAC=25°,$$∠OBA=\frac 1 2∠ABC=35°$
∴ ∠AOB=180°-25°-35°=120°
解:连接OD,OE,OF
∵ AC、AB、BC为⊙O的切线
∴ OD⊥AC,OE⊥AB,OF⊥BC
∴ ∠ODC=∠OFC=90°
∵ ∠ABC=70°,∠BAC=50
°∴ ∠C=180°-70°-50°=60°
∴ ∠DOF=360°-90°-90°-60°=120°
∴$ ∠DEF=\frac 1 2∠DOF=60°$
∵ OD=OE=OF∴ AO平分∠CAB,BO平分∠CBA
∴$ ∠OAB=\frac 12∠BAC=25°,$$∠OBA=\frac 1 2∠ABC=35°$
∴ ∠AOB=180°-25°-35°=120°

解析:
连接OD、OF。
在△ABC中,∠ABC=70°,∠BAC=50°,则∠ACB=180°-70°-50°=60°。
∵内切圆O分别切AC、BC于点D、F,
∴OD⊥AC,OF⊥BC,∠ODC=∠OFC=90°。
在四边形ODCF中,∠DOF=360°-∠ODC-∠OFC-∠C=360°-90°-90°-60°=120°。
∵∠DEF是圆周角,∠DOF是圆心角,且它们所对的弧都是$\overset{\frown}{DF}$,
∴∠DEF=$\frac{1}{2}$∠DOF=$\frac{1}{2}$×120°=60°。
∵O是△ABC的内心,
∴OA、OB分别平分∠BAC、∠ABC。
∠OAB=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×50°=25°,∠OBA=$\frac{1}{2}$∠ABC=$\frac{1}{2}$×70°=35°。
在△AOB中,∠AOB=180°-∠OAB-∠OBA=180°-25°-35°=120°。
∠DEF=60°,∠AOB=120°。
在△ABC中,∠ABC=70°,∠BAC=50°,则∠ACB=180°-70°-50°=60°。
∵内切圆O分别切AC、BC于点D、F,
∴OD⊥AC,OF⊥BC,∠ODC=∠OFC=90°。
在四边形ODCF中,∠DOF=360°-∠ODC-∠OFC-∠C=360°-90°-90°-60°=120°。
∵∠DEF是圆周角,∠DOF是圆心角,且它们所对的弧都是$\overset{\frown}{DF}$,
∴∠DEF=$\frac{1}{2}$∠DOF=$\frac{1}{2}$×120°=60°。
∵O是△ABC的内心,
∴OA、OB分别平分∠BAC、∠ABC。
∠OAB=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×50°=25°,∠OBA=$\frac{1}{2}$∠ABC=$\frac{1}{2}$×70°=35°。
在△AOB中,∠AOB=180°-∠OAB-∠OBA=180°-25°-35°=120°。
∠DEF=60°,∠AOB=120°。