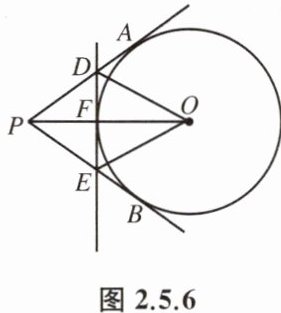
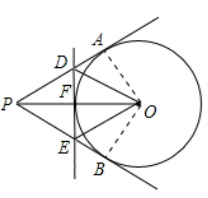
例1 如图2.5.6,⊙O的半径为6 cm,过圆外一点P引圆的切线PA、PB,切点分别为A、B,连接PO交⊙O于点F,过点F作⊙O的切线分别交PA、PB于点D、E,已知PO= 10 cm,求△PED的周长.

答案:
解:连接AO,BO
∵ PA,PB为⊙O的切线
∴ PA=PB,∠PAO=∠PBO=90°
在Rt△PAO中,∵ PO=10cm,AO=6cm
∴$ PA={\sqrt {{PO}^{2}-{AO}^{2}}=8}cm$
∴ PB=PA=8cm
∵ DF,DA为⊙O的切线,EF,EB为⊙O的切线
∴ DF=DA,EF=EB
∴ {C}_{△PED}=PD+DF+PE+EF
=PD+DA+PE+EB
=PA+PB=16cm∴ △PED的周长为$16\ \mathrm {cm}.$
解:连接AO,BO
∵ PA,PB为⊙O的切线
∴ PA=PB,∠PAO=∠PBO=90°
在Rt△PAO中,∵ PO=10cm,AO=6cm
∴$ PA={\sqrt {{PO}^{2}-{AO}^{2}}=8}cm$
∴ PB=PA=8cm
∵ DF,DA为⊙O的切线,EF,EB为⊙O的切线
∴ DF=DA,EF=EB
∴ {C}_{△PED}=PD+DF+PE+EF
=PD+DA+PE+EB
=PA+PB=16cm∴ △PED的周长为$16\ \mathrm {cm}.$

解析:
连接OA,因为PA是⊙O的切线,所以OA⊥PA。在Rt△POA中,OA=6cm,PO=10cm,由勾股定理得PA=$\sqrt{PO^2 - OA^2}=\sqrt{10^2 - 6^2}=8$cm。
因为PA、PB是⊙O的切线,所以PA=PB=8cm。
因为DA、DF是⊙O的切线,所以DA=DF;同理EB=EF。
△PED的周长=PD+DE+PE=PD+DF+EF+PE=PD+DA+EB+PE=PA+PB=8+8=16cm。
16 cm
因为PA、PB是⊙O的切线,所以PA=PB=8cm。
因为DA、DF是⊙O的切线,所以DA=DF;同理EB=EF。
△PED的周长=PD+DE+PE=PD+DF+EF+PE=PD+DA+EB+PE=PA+PB=8+8=16cm。
16 cm
例2 如图2.5.7,△ABC的内切圆⊙O与边BC、CA、AB分别相切于点D、E、F,且AB= 9 cm,BC= 14 cm,CA= 13 cm.求AF、BD、CE的长.


答案:解:∵ BC、CA、AB为⊙O的切线,切点分别为点D、E、F
∴ AE=AF,BD=BF,CD=CE
设$AE=AF=x\ \mathrm {cm},$$BD=BF=y\ \mathrm {cm},$$CD=CE=z\ \mathrm {cm}$
依题意得,${{\begin{cases} {{x+y=9}} \\ {y+z=14} \\ {x+z=13} \end{cases}}}$
解得,${{\begin{cases} {{x=4}} \\ {y=5} \\ {z=9} \end{cases}}}$
∴ AF的长为4cm,BD的长为5cm,CE的长为9cm.
∴ AE=AF,BD=BF,CD=CE
设$AE=AF=x\ \mathrm {cm},$$BD=BF=y\ \mathrm {cm},$$CD=CE=z\ \mathrm {cm}$
依题意得,${{\begin{cases} {{x+y=9}} \\ {y+z=14} \\ {x+z=13} \end{cases}}}$
解得,${{\begin{cases} {{x=4}} \\ {y=5} \\ {z=9} \end{cases}}}$
∴ AF的长为4cm,BD的长为5cm,CE的长为9cm.
解析:
设AF=x cm,BD=y cm,CE=z cm。
因为⊙O与△ABC的三边相切,所以AE=AF=x cm,BF=BD=y cm,CD=CE=z cm。
由题意得:
$\begin{cases}x + y = 9 \\y + z = 14 \\x + z = 13\end{cases}$
将三个方程相加得:2(x + y + z)=36,即x + y + z=18。
用x + y + z=18分别减去上述三个方程:
z=18 - 9=9,x=18 - 14=4,y=18 - 13=5。
AF=4 cm,BD=5 cm,CE=9 cm。
因为⊙O与△ABC的三边相切,所以AE=AF=x cm,BF=BD=y cm,CD=CE=z cm。
由题意得:
$\begin{cases}x + y = 9 \\y + z = 14 \\x + z = 13\end{cases}$
将三个方程相加得:2(x + y + z)=36,即x + y + z=18。
用x + y + z=18分别减去上述三个方程:
z=18 - 9=9,x=18 - 14=4,y=18 - 13=5。
AF=4 cm,BD=5 cm,CE=9 cm。