1. 一根钢管放在V形架内,其截面图如图所示,O为钢管截面的圆心,已知钢管的半径为25 cm,∠MPN= 60°,则OP=
50
cm.答案:50
解析:
连接OM,ON。
因为钢管与V形架相切,所以OM⊥PM,ON⊥PN,即∠OMP=∠ONP=90°。
又因为OM=ON=25cm(半径),OP为公共边,所以Rt△OMP≌Rt△ONP(HL),则∠OPM=∠OPN=∠MPN/2=30°。
在Rt△OMP中,sin∠OPM=OM/OP,即sin30°=25/OP。
因为sin30°=1/2,所以1/2=25/OP,解得OP=50cm。
50
因为钢管与V形架相切,所以OM⊥PM,ON⊥PN,即∠OMP=∠ONP=90°。
又因为OM=ON=25cm(半径),OP为公共边,所以Rt△OMP≌Rt△ONP(HL),则∠OPM=∠OPN=∠MPN/2=30°。
在Rt△OMP中,sin∠OPM=OM/OP,即sin30°=25/OP。
因为sin30°=1/2,所以1/2=25/OP,解得OP=50cm。
50
2. 如图,AB、AC是⊙O的切线,点D在⊙O上,且∠D= 70°,则∠A= ______.
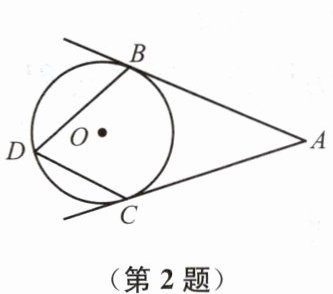

40°
答案:40°
解析:
连接OB、OC。
∵AB、AC是⊙O的切线,
∴OB⊥AB,OC⊥AC,
∴∠OBA=∠OCA=90°。
∵∠D=70°,
∴∠BOC=2∠D=140°。
在四边形ABOC中,∠A+∠OBA+∠OCA+∠BOC=360°,
∴∠A=360°-∠OBA-∠OCA-∠BOC=360°-90°-90°-140°=40°。
40°
∵AB、AC是⊙O的切线,
∴OB⊥AB,OC⊥AC,
∴∠OBA=∠OCA=90°。
∵∠D=70°,
∴∠BOC=2∠D=140°。
在四边形ABOC中,∠A+∠OBA+∠OCA+∠BOC=360°,
∴∠A=360°-∠OBA-∠OCA-∠BOC=360°-90°-90°-140°=40°。
40°
3. 如图,在Rt△EBC中,∠CBE= 90°,点A在边EB上,以AB为直径的⊙O与CE相切于点D,若BC= 6,EB= 8,则⊙O的半径为
3
.答案:3
解析:
连接OD,设⊙O的半径为$ r $,则$ OA=OB=OD=r $。
因为$ EB=8 $,所以$ OE=EB - OB=8 - r $。
因为$ \angle CBE=90^\circ $,$ BC=6 $,$ EB=8 $,所以$ EC=\sqrt{EB^2 + BC^2}=\sqrt{8^2 + 6^2}=10 $。
因为CE是⊙O的切线,D为切点,所以$ OD \perp CE $,即$ \angle ODE=90^\circ $。
又因为$ \angle CBE=90^\circ $,$ \angle E=\angle E $,所以$ \triangle EOD \sim \triangle ECB $。
所以$ \frac{OD}{BC}=\frac{OE}{EC} $,即$ \frac{r}{6}=\frac{8 - r}{10} $。
解得$ 10r = 6(8 - r) $,$ 10r = 48 - 6r $,$ 16r = 48 $,$ r = 3 $。
3
因为$ EB=8 $,所以$ OE=EB - OB=8 - r $。
因为$ \angle CBE=90^\circ $,$ BC=6 $,$ EB=8 $,所以$ EC=\sqrt{EB^2 + BC^2}=\sqrt{8^2 + 6^2}=10 $。
因为CE是⊙O的切线,D为切点,所以$ OD \perp CE $,即$ \angle ODE=90^\circ $。
又因为$ \angle CBE=90^\circ $,$ \angle E=\angle E $,所以$ \triangle EOD \sim \triangle ECB $。
所以$ \frac{OD}{BC}=\frac{OE}{EC} $,即$ \frac{r}{6}=\frac{8 - r}{10} $。
解得$ 10r = 6(8 - r) $,$ 10r = 48 - 6r $,$ 16r = 48 $,$ r = 3 $。
3
4. 如图,在矩形ABCD中,AB= 4,AD= 5,AD、AB、BC分别与⊙O相切于点E、F、G,过点D作⊙O的切线,交BC于点M,切点为N,则DM的长为
$\frac{13}{3}$
.答案:$\frac{13}{3}$
解析:
设⊙O半径为$r$,连接OE、OF、OG,OE⊥AD,OF⊥AB,OG⊥BC,四边形AFOE、FBGO为矩形,AF=OE=$r$,BF=OG=$r$,AB=AF+BF=$2r$=4,$r$=2,OE=2,AE=OF=2,ED=AD-AE=5-2=3,设CM=$x$,则BM=BC-CM=5-$x$,DM切⊙O于N,DN=DE=3,MN=MG=BM-BG=5-$x$-2=3-$x$,CD=4,在Rt△DCM中,$DM^2=CD^2+CM^2$,$(DN+MN)^2=4^2+x^2$,$(3+3-x)^2=16+x^2$,$(6-x)^2=16+x^2$,36-12x+$x^2$=16+$x^2$,12x=20,$x=\frac{5}{3}$,DM=6-$\frac{5}{3}$=$\frac{13}{3}$
$\frac{13}{3}$
$\frac{13}{3}$
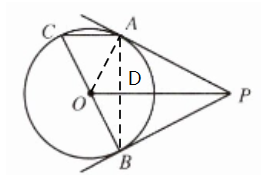
5. 如图,BC是⊙O的直径,P为⊙O外的一点,PA、PB为⊙O的切线,切点分别为A、B.试说明AC//OP.


答案:
证明:连接OA,AB,AB与OP交于点D.
∵PA,PB为$\odot O$的切线
∴PA=PB
∴点P在AB的垂直平分线上
∵OA=OB
∴点O在AB的垂直平分线上
∴OP垂直平分AB
∴∠BDO=90°
∵BC为$\odot O$的直径
∴∠BAC=90°
∴∠BDO=∠BAC
∴AC//OP
证明:连接OA,AB,AB与OP交于点D.
∵PA,PB为$\odot O$的切线
∴PA=PB
∴点P在AB的垂直平分线上
∵OA=OB
∴点O在AB的垂直平分线上
∴OP垂直平分AB
∴∠BDO=90°
∵BC为$\odot O$的直径
∴∠BAC=90°
∴∠BDO=∠BAC
∴AC//OP
