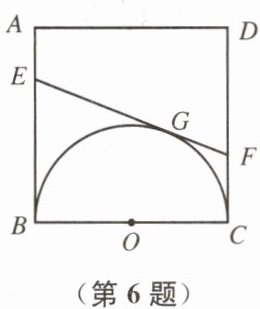
6. 如图,正方形ABCD的边长为a,以BC为直径向正方形内画半圆,EF切半圆于点G,分别交AB、CD于点E、F.
(1) 求四边形AEFD的周长;
(2) 已知∠BEF= 60°,求四边形EBCF的周长.
(1) 求四边形AEFD的周长;
(2) 已知∠BEF= 60°,求四边形EBCF的周长.

答案:
解:( 1 ) ∵四边形ABCD为正方形
∴∠ABC=∠DCB=90°∴EB,FC为半圆的切线
∵EF与半圆相切于点G
∴EB=EG,FC=FG.
∴C_{四边形AEFD}=AE+EG+FG+FD+AD
=( AE+EB ) +( FC+FD ) +AD
=AB+CD+AD
=3a,
即四边形AEFD的周长为3a
解:( 2 ) 过点F作FH⊥AB,垂足为点H
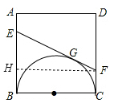
在Rt△FHE中,
∵∠BEF=60°
∴∠HFE=90°-60°=30°
∴EF=2EH,$FH=\sqrt{3}EH$
∵FH=BC=a
∴$EH=\frac {\sqrt{3}}{3}a,$
$EF=\frac {2\sqrt{3}}{3}a$
∴C_{四边形EBCF}
=EB+CF+EF+BC
=EG+FG+EF+BC
=2EF+BC
$=(\frac {4\sqrt{3}}{3}+1)a,$
即边形EBCF的周长为$(\frac {4\sqrt{3}}{3}+1)a $
解:( 1 ) ∵四边形ABCD为正方形
∴∠ABC=∠DCB=90°∴EB,FC为半圆的切线
∵EF与半圆相切于点G
∴EB=EG,FC=FG.
∴C_{四边形AEFD}=AE+EG+FG+FD+AD
=( AE+EB ) +( FC+FD ) +AD
=AB+CD+AD
=3a,
即四边形AEFD的周长为3a
解:( 2 ) 过点F作FH⊥AB,垂足为点H

在Rt△FHE中,
∵∠BEF=60°
∴∠HFE=90°-60°=30°
∴EF=2EH,$FH=\sqrt{3}EH$
∵FH=BC=a
∴$EH=\frac {\sqrt{3}}{3}a,$
$EF=\frac {2\sqrt{3}}{3}a$
∴C_{四边形EBCF}
=EB+CF+EF+BC
=EG+FG+EF+BC
=2EF+BC
$=(\frac {4\sqrt{3}}{3}+1)a,$
即边形EBCF的周长为$(\frac {4\sqrt{3}}{3}+1)a $
解析:
(1)设半圆的圆心为O,半径为$\frac{a}{2}$,设$BE = x$,$CF = y$。因为EF切半圆于G,所以$EG = BE = x$,$FG = CF = y$。在直角梯形EBCF中,$EF = x + y$,高$BC = a$,下底$BC = a$,上底$EF$在两腰之间,过F作$FH \perp AB$于H,则$EH = x - y$,$FH = a$。在$Rt\triangle EHF$中,$(x + y)^2 = a^2 + (x - y)^2$,化简得$4xy = a^2$。四边形AEFD的周长为$AE + EF + FD + DA = (a - x) + (x + y) + (a - y) + a = 3a$。
(2)因为$\angle BEF = 60^\circ$,在$Rt\triangle EHF$中,$\cos 60^\circ = \frac{EH}{EF} = \frac{x - y}{x + y} = \frac{1}{2}$,即$2(x - y) = x + y$,得$x = 3y$。由(1)知$4xy = a^2$,将$x = 3y$代入得$4 × 3y × y = a^2$,$y = \frac{a}{2\sqrt{3}} = \frac{\sqrt{3}a}{6}$,$x = \frac{\sqrt{3}a}{2}$。四边形EBCF的周长为$BE + BC + CF + EF = x + a + y + (x + y) = 2x + 2y + a = 2(x + y) + a$。由$x = 3y$,$x + y = 4y = \frac{2\sqrt{3}a}{3}$,所以周长为$2 × \frac{2\sqrt{3}a}{3} + a = \frac{4\sqrt{3}a}{3} + a = (\frac{4\sqrt{3}}{3} + 1)a$。
(2)因为$\angle BEF = 60^\circ$,在$Rt\triangle EHF$中,$\cos 60^\circ = \frac{EH}{EF} = \frac{x - y}{x + y} = \frac{1}{2}$,即$2(x - y) = x + y$,得$x = 3y$。由(1)知$4xy = a^2$,将$x = 3y$代入得$4 × 3y × y = a^2$,$y = \frac{a}{2\sqrt{3}} = \frac{\sqrt{3}a}{6}$,$x = \frac{\sqrt{3}a}{2}$。四边形EBCF的周长为$BE + BC + CF + EF = x + a + y + (x + y) = 2x + 2y + a = 2(x + y) + a$。由$x = 3y$,$x + y = 4y = \frac{2\sqrt{3}a}{3}$,所以周长为$2 × \frac{2\sqrt{3}a}{3} + a = \frac{4\sqrt{3}a}{3} + a = (\frac{4\sqrt{3}}{3} + 1)a$。
7. 如图,AC⊥BC,垂足为C,BC= 4,AC= 3,⊙O与直线AC、BC、AB分别相切于点D、E、F.求⊙O的半径.


答案:
解:∵ AC⊥BC,
∴∠ACB = 90°,
∵ BC=4,AC= 3,
∴AB= 5
连接OD、OE;
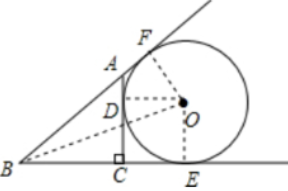
∴AC、BE是O的切线,
∴∠ODC=∠OEC=∠DCE= 90°;
∴四边形ODCE是矩形;
∵OD = OE,
∴矩形ODCE是正方形;
即OE= OD= CD;
设CD= CE=x,
则AD= AF=3- x;
连接OB, OF,
由勾股定理得:\
$BF^2 = OB^2 - OF^2,$\
$BE^2 =OB^2 - OE^2$
∵ OB= OB, OF= OE,
∴ BF= BE,
则BA+ AF= BC +CE,
\ 5+3-x=4+x,
即x = 2;
故⊙O的半径为2.
解:∵ AC⊥BC,
∴∠ACB = 90°,
∵ BC=4,AC= 3,
∴AB= 5
连接OD、OE;

∴AC、BE是O的切线,
∴∠ODC=∠OEC=∠DCE= 90°;
∴四边形ODCE是矩形;
∵OD = OE,
∴矩形ODCE是正方形;
即OE= OD= CD;
设CD= CE=x,
则AD= AF=3- x;
连接OB, OF,
由勾股定理得:\
$BF^2 = OB^2 - OF^2,$\
$BE^2 =OB^2 - OE^2$
∵ OB= OB, OF= OE,
∴ BF= BE,
则BA+ AF= BC +CE,
\ 5+3-x=4+x,
即x = 2;
故⊙O的半径为2.
解析:
连接OD、OE、OF。
∵AC⊥BC,⊙O与AC、BC、AB分别相切于D、E、F,
∴OD⊥AC,OE⊥BC,OD=OE=OF=r。
∴四边形CDOE是正方形,CD=CE=r。
∵AC=3,BC=4,
∴AD=AC-CD=3-r,BE=BC-CE=4-r。
∵AD=AF,BE=BF,
∴AF=3-r,BF=4-r。
在Rt△ABC中,AB=$\sqrt{AC^2+BC^2}=\sqrt{3^2+4^2}=5$。
∵AF+BF=AB,
∴(3-r)+(4-r)=5,
解得r=1。
1
∵AC⊥BC,⊙O与AC、BC、AB分别相切于D、E、F,
∴OD⊥AC,OE⊥BC,OD=OE=OF=r。
∴四边形CDOE是正方形,CD=CE=r。
∵AC=3,BC=4,
∴AD=AC-CD=3-r,BE=BC-CE=4-r。
∵AD=AF,BE=BF,
∴AF=3-r,BF=4-r。
在Rt△ABC中,AB=$\sqrt{AC^2+BC^2}=\sqrt{3^2+4^2}=5$。
∵AF+BF=AB,
∴(3-r)+(4-r)=5,
解得r=1。
1
8. 如图,⊙O与四边形ABCD各边都相切,切点分别为E、F、G、H,若四边形ABCD的周长为36 cm,则AB+CD=
18
cm.答案:18
解析:
∵⊙O与四边形ABCD各边都相切,
∴AE=AH,BE=BF,CF=CG,DG=DH,
∴AB+CD=AE+BE+CG+DG=AH+BF+CF+DH=AD+BC,
∵四边形ABCD的周长为36 cm,
∴AB+BC+CD+AD=36 cm,
∴2(AB+CD)=36 cm,
∴AB+CD=18 cm.
18
9. 如图①,将一个量角器与一张等腰三角形纸片ABC放置成轴对称图形.∠ACB= 90°,CD⊥AB,垂足为D,半圆(量角器)的圆心与点D重合,测得CE= 5 cm;将半圆(量角器)沿DC方向平移2 cm,恰与△ABC的边AC、BC相切,如图②,则边AB的长为
$16+6 \sqrt{2}$
cm.答案:$16+6 \sqrt{2},$