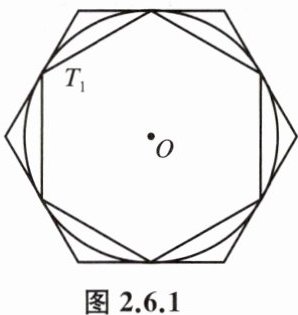
例 1 (1)如图 2.6.1,已知$\odot O的半径为r$,其内接正六边形与外切正六边形的边长分别为$a、b$,面积分别为$S_{1}$、$S_{2}$.有下列结论:①$r:a= 1:1$;②$r:b= \sqrt{3}:2$;③$a:b= 1:\sqrt{3}$;④$S_{1}:S_{2}= 3:4$.其中正确的有
(2)下列命题:① 各边都相等的圆内接多边形是正多边形;② 各角都相等的圆内接多边形是正多边形;③ 正多边形都有内切圆和外接圆,且这两个圆是同心圆;④ 正多边形既是轴对称图形又是中心对称图形.其中真命题有
①②④
.(填序号)
(2)下列命题:① 各边都相等的圆内接多边形是正多边形;② 各角都相等的圆内接多边形是正多边形;③ 正多边形都有内切圆和外接圆,且这两个圆是同心圆;④ 正多边形既是轴对称图形又是中心对称图形.其中真命题有
①③
.(填序号)答案:①②④
①③.
①③.
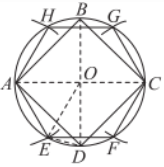
例 2 已知:如图 2.6.2,$A是\odot O$上的一点.
(1)作$\odot O的内接正方形ABCD和内接正六边形AEFCGH$.
(2)在(1)的作图中,如果点$E在\widehat{AD}$上,那么线段$DE是\odot O$内接正十二边形的一边吗?为什么?

(1)作$\odot O的内接正方形ABCD和内接正六边形AEFCGH$.
(2)在(1)的作图中,如果点$E在\widehat{AD}$上,那么线段$DE是\odot O$内接正十二边形的一边吗?为什么?

答案:
解:(1)作法:
①作直径AC;
②作直径BD⊥AC;
③依次连接A、B、C、D四点,
四边形ABCD即为⊙O的内接正方形;
④分别以A、C为圆心,以OA长为半径作弧,交⊙O于E、H、F、G;
⑤顺次连接A、E、F、C、G、H各点.
六边形AEFCGH即为⊙O的内接正六边形.
(2)证明:连接OE、DE.
∵$∠AOD=\frac {360°}{4}=90°,$$∠AOE=\frac {360°}{6}=60°,$
∴∠DOE=∠AOD-∠AOE=90°-60°=30°,
∴DE为⊙O的内接正十二边形的一边.
解:(1)作法:
①作直径AC;
②作直径BD⊥AC;
③依次连接A、B、C、D四点,
四边形ABCD即为⊙O的内接正方形;
④分别以A、C为圆心,以OA长为半径作弧,交⊙O于E、H、F、G;
⑤顺次连接A、E、F、C、G、H各点.
六边形AEFCGH即为⊙O的内接正六边形.
(2)证明:连接OE、DE.
∵$∠AOD=\frac {360°}{4}=90°,$$∠AOE=\frac {360°}{6}=60°,$
∴∠DOE=∠AOD-∠AOE=90°-60°=30°,
∴DE为⊙O的内接正十二边形的一边.

解析:
(1)作图步骤:
1. 连接 $AO$ 并延长交 $\odot O$ 于点 $C$;
2. 作 $AC$ 的垂直平分线交 $\odot O$ 于点 $B$、$D$,连接 $AB$、$BC$、$CD$、$DA$,四边形 $ABCD$ 即为内接正方形;
3. 以 $A$ 为圆心,$AO$ 为半径画弧交 $\odot O$ 于点 $E$、$H$;
4. 分别以 $E$、$H$ 为圆心,$AO$ 为半径画弧交 $\odot O$ 于点 $F$、$G$,连接 $AE$、$EF$、$FC$、$CG$、$GH$、$HA$,六边形 $AEFCGH$ 即为内接正六边形。
(2)是。
理由:设 $\odot O$ 半径为 $R$,内接正方形中心角 $\angle AOD = \frac{360^\circ}{4} = 90^\circ$,内接正六边形中心角 $\angle AOE = \frac{360^\circ}{6} = 60^\circ$,则 $\angle DOE = \angle AOD - \angle AOE = 90^\circ - 60^\circ = 30^\circ$,$\frac{360^\circ}{30^\circ} = 12$,故 $DE$ 是内接正十二边形的一边。
1. 连接 $AO$ 并延长交 $\odot O$ 于点 $C$;
2. 作 $AC$ 的垂直平分线交 $\odot O$ 于点 $B$、$D$,连接 $AB$、$BC$、$CD$、$DA$,四边形 $ABCD$ 即为内接正方形;
3. 以 $A$ 为圆心,$AO$ 为半径画弧交 $\odot O$ 于点 $E$、$H$;
4. 分别以 $E$、$H$ 为圆心,$AO$ 为半径画弧交 $\odot O$ 于点 $F$、$G$,连接 $AE$、$EF$、$FC$、$CG$、$GH$、$HA$,六边形 $AEFCGH$ 即为内接正六边形。
(2)是。
理由:设 $\odot O$ 半径为 $R$,内接正方形中心角 $\angle AOD = \frac{360^\circ}{4} = 90^\circ$,内接正六边形中心角 $\angle AOE = \frac{360^\circ}{6} = 60^\circ$,则 $\angle DOE = \angle AOD - \angle AOE = 90^\circ - 60^\circ = 30^\circ$,$\frac{360^\circ}{30^\circ} = 12$,故 $DE$ 是内接正十二边形的一边。