1. 半径相等的圆的内接正三角形、正方形、正六边形边长之比为(
A.$1:\sqrt{2}:\sqrt{3}$
B.$\sqrt{3}:\sqrt{2}:1$
C.$3:2:1$
D.$1:2:3$
B
)A.$1:\sqrt{2}:\sqrt{3}$
B.$\sqrt{3}:\sqrt{2}:1$
C.$3:2:1$
D.$1:2:3$
答案:B
解析:
设圆的半径为$R$。
对于圆的内接正三角形:边长$a_3 = 2R\sin\frac{\pi}{3} = 2R×\frac{\sqrt{3}}{2} = \sqrt{3}R$。
对于圆的内接正方形:边长$a_4 = 2R\sin\frac{\pi}{4} = 2R×\frac{\sqrt{2}}{2} = \sqrt{2}R$。
对于圆的内接正六边形:边长$a_6 = 2R\sin\frac{\pi}{6} = 2R×\frac{1}{2} = R$。
所以边长之比为$a_3:a_4:a_6 = \sqrt{3}R:\sqrt{2}R:R = \sqrt{3}:\sqrt{2}:1$。
B
对于圆的内接正三角形:边长$a_3 = 2R\sin\frac{\pi}{3} = 2R×\frac{\sqrt{3}}{2} = \sqrt{3}R$。
对于圆的内接正方形:边长$a_4 = 2R\sin\frac{\pi}{4} = 2R×\frac{\sqrt{2}}{2} = \sqrt{2}R$。
对于圆的内接正六边形:边长$a_6 = 2R\sin\frac{\pi}{6} = 2R×\frac{1}{2} = R$。
所以边长之比为$a_3:a_4:a_6 = \sqrt{3}R:\sqrt{2}R:R = \sqrt{3}:\sqrt{2}:1$。
B
2. 等边三角形的内切圆半径、外接圆半径和高的比为(
A.$1:\sqrt{2}:\sqrt{3}$
B.$1:2:\sqrt{3}$
C.$1:\sqrt{3}:2$
D.$1:2:3$
D
)A.$1:\sqrt{2}:\sqrt{3}$
B.$1:2:\sqrt{3}$
C.$1:\sqrt{3}:2$
D.$1:2:3$
答案:D
解析:
设等边三角形的边长为$a$。
其高$h = \frac{\sqrt{3}}{2}a$。
外接圆半径$R = \frac{\sqrt{3}}{3}a$。
内切圆半径$r = \frac{\sqrt{3}}{6}a$。
则$r:R:h = \frac{\sqrt{3}}{6}a : \frac{\sqrt{3}}{3}a : \frac{\sqrt{3}}{2}a = 1:2:3$
D
其高$h = \frac{\sqrt{3}}{2}a$。
外接圆半径$R = \frac{\sqrt{3}}{3}a$。
内切圆半径$r = \frac{\sqrt{3}}{6}a$。
则$r:R:h = \frac{\sqrt{3}}{6}a : \frac{\sqrt{3}}{3}a : \frac{\sqrt{3}}{2}a = 1:2:3$
D
3. 如图,扳手中的正六边形螺帽的边长为$a$,则扳手的开口$b$最小应是
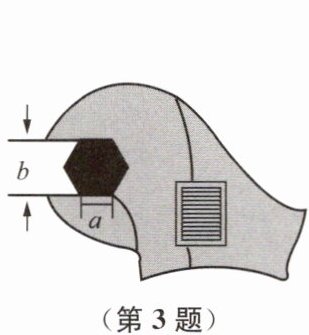
$\sqrt{3}a$
(用含$a$的代数式表示).
答案:$\sqrt{3}a$
解析:
正六边形螺帽的扳手开口$b$为其对边距离。正六边形可分割为六个等边三角形,边长为$a$,每个内角为$120^\circ$。连接对边顶点,构成等腰三角形,腰长为$a$,顶角$120^\circ$。作底边上的高,将其分为两个含$60^\circ$角的直角三角形,高为$a\sin60^\circ=\frac{\sqrt{3}}{2}a$,对边距离$b=2×\frac{\sqrt{3}}{2}a=\sqrt{3}a$。
$\sqrt{3}a$
$\sqrt{3}a$
4. 如图,若干个相同的正五边形排成环状.图中已经排好了前3个五边形,还需

7
个五边形完成这一圆环.
答案:7
解析:
正五边形每个内角为$\frac{(5 - 2)×180^\circ}{5} = 108^\circ$,每个外角为$180^\circ - 108^\circ = 72^\circ$。圆环一周为$360^\circ$,所需五边形总数为$\frac{360^\circ}{72^\circ} = 10$个。已排好3个,还需$10 - 3 = 7$个。
7
7
5. 如图,$\triangle ABC为\odot O$的内接三角形,$AB= 1$,$\angle C= 30^{\circ}$,则$\odot O$的内接正方形的面积为
2
.答案:2
解析:
连接$OA$,$OB$。
$\because \angle C = 30^\circ$,
$\therefore \angle AOB = 2\angle C = 60^\circ$。
$\because OA = OB$,
$\therefore \triangle AOB$为等边三角形,$OA = AB = 1$,即$\odot O$半径$r = 1$。
设$\odot O$的内接正方形边长为$a$,则正方形对角线长为$2r = 2$。
由勾股定理:$a^2 + a^2 = 2^2$,解得$a^2 = 2$。
故$\odot O$的内接正方形面积为$2$。
$2$
$\because \angle C = 30^\circ$,
$\therefore \angle AOB = 2\angle C = 60^\circ$。
$\because OA = OB$,
$\therefore \triangle AOB$为等边三角形,$OA = AB = 1$,即$\odot O$半径$r = 1$。
设$\odot O$的内接正方形边长为$a$,则正方形对角线长为$2r = 2$。
由勾股定理:$a^2 + a^2 = 2^2$,解得$a^2 = 2$。
故$\odot O$的内接正方形面积为$2$。
$2$
6. 如图,在正五边形$ABCDE$中,对角线$BD、CE相交于点P$.
求证:四边形$ABPE$是菱形.

求证:四边形$ABPE$是菱形.

答案:证明:由正五边形ABCDE知,每个顶角的度数为108°,
在△BCD中,BC=CD
∴∠CBD=∠CDB=(180°-108°)÷2=36°
∴∠ABD=∠ABC-∠CBD=108°-36°=72°
∴∠ABD+∠A=72°+108°=180°
∴AE//BD,
同理,AB//CE
∴四边形ABPE是平行四边形
又∵AB=AE
∴四边形ABPE是菱形
在△BCD中,BC=CD
∴∠CBD=∠CDB=(180°-108°)÷2=36°
∴∠ABD=∠ABC-∠CBD=108°-36°=72°
∴∠ABD+∠A=72°+108°=180°
∴AE//BD,
同理,AB//CE
∴四边形ABPE是平行四边形
又∵AB=AE
∴四边形ABPE是菱形