2. 将直径为 60 cm 的圆形铁皮制成三个相同的圆锥容器的侧面(不浪费材料,不计接缝处的材料损耗),每个圆锥容器的底面半径为(
A.10 cm
B.30 cm
C.40 cm
D.300 cm
A
)A.10 cm
B.30 cm
C.40 cm
D.300 cm
答案:A
解析:
圆形铁皮的直径为$60\,cm$,则其半径$R = 30\,cm$,周长$C = 2\pi R=60\pi\,cm$。
将其制成三个相同圆锥的侧面,每个圆锥的底面周长$c=\frac{C}{3}=\frac{60\pi}{3}=20\pi\,cm$。
设每个圆锥底面半径为$r$,由$c = 2\pi r$得$2\pi r=20\pi$,解得$r = 10\,cm$。
A
将其制成三个相同圆锥的侧面,每个圆锥的底面周长$c=\frac{C}{3}=\frac{60\pi}{3}=20\pi\,cm$。
设每个圆锥底面半径为$r$,由$c = 2\pi r$得$2\pi r=20\pi$,解得$r = 10\,cm$。
A
3. 如图,把一张圆心角为 $120^\circ$,半径为 9 cm 的扇形纸片用胶水粘贴制作一个底面半径为 2 cm 的圆锥侧面,该圆锥侧面上粘贴部分的面积是(
A.$8\pi$
B.$9\pi$
C.$19\pi$
D.$27\pi$
B
)A.$8\pi$
B.$9\pi$
C.$19\pi$
D.$27\pi$
答案:B
解析:
扇形弧长:$\frac{120^\circ}{360^\circ} × 2\pi × 9 = 6\pi$
圆锥底面周长:$2\pi × 2 = 4\pi$
粘贴部分弧长:$6\pi - 4\pi = 2\pi$
粘贴部分面积:$\frac{1}{2} × 2\pi × 9 = 9\pi$
B
圆锥底面周长:$2\pi × 2 = 4\pi$
粘贴部分弧长:$6\pi - 4\pi = 2\pi$
粘贴部分面积:$\frac{1}{2} × 2\pi × 9 = 9\pi$
B
4. 一个圆锥的侧面积是底面积的 3 倍,则圆锥侧面展开图的圆心角是(
A.$90^\circ$
B.$120^\circ$
C.$150^\circ$
D.$180^\circ$
180
)A.$90^\circ$
B.$120^\circ$
C.$150^\circ$
D.$180^\circ$
答案:180
解析:
设圆锥底面半径为$r$,母线长为$l$,侧面展开图的圆心角为$n^\circ$。
底面积$S_底=\pi r^2$,侧面积$S_侧=\pi rl$。
由题意$S_侧=3S_底$,即$\pi rl = 3\pi r^2$,化简得$l=3r$。
圆锥侧面展开图弧长等于底面周长,$\frac{n\pi l}{180}=2\pi r$,将$l=3r$代入得$\frac{n\pi \cdot 3r}{180}=2\pi r$,解得$n=120$。
B
底面积$S_底=\pi r^2$,侧面积$S_侧=\pi rl$。
由题意$S_侧=3S_底$,即$\pi rl = 3\pi r^2$,化简得$l=3r$。
圆锥侧面展开图弧长等于底面周长,$\frac{n\pi l}{180}=2\pi r$,将$l=3r$代入得$\frac{n\pi \cdot 3r}{180}=2\pi r$,解得$n=120$。
B
5. 在综合实践活动课上,小明同学用纸板制作了一个圆锥形漏斗模型,它的底面半径为 6 cm,高为 8 cm,这个圆锥漏斗的侧面积是
60π
$cm^2$.答案:60π
解析:
圆锥的母线长为 $\sqrt{6^2 + 8^2} = 10\ cm$,侧面积为 $\pi × 6 × 10 = 60\pi\ cm^2$。
$60\pi$
$60\pi$
6. 用半径为 9,圆心角为 $120^\circ$的扇形围成一个圆锥的侧面(接缝忽略不计),这个圆锥的底面半径是
3
.答案:3
解析:
扇形的弧长公式为$l = \frac{n\pi R}{180}$(其中$n$为圆心角度数,$R$为扇形半径),则该扇形的弧长为:$\frac{120\pi×9}{180} = 6\pi$。
圆锥底面周长等于侧面展开图的扇形弧长,设圆锥底面半径为$r$,底面周长为$2\pi r$,所以$2\pi r = 6\pi$,解得$r = 3$。
3
圆锥底面周长等于侧面展开图的扇形弧长,设圆锥底面半径为$r$,底面周长为$2\pi r$,所以$2\pi r = 6\pi$,解得$r = 3$。
3
7. 如图,从直径为 6 cm 的圆形铁皮上剪下一个圆心角为 $90^\circ$的扇形铁皮后,从余下的铁皮上剪出一个最大的圆形铁皮,刚好能围成一个圆锥,这个圆锥的底面周长是
$2\pi$
.答案:$2\pi$
解析:
圆形铁皮直径为6 cm,半径$ R = 3 \, cm $。
剪下圆心角$ 90^\circ $的扇形,扇形半径为$ 3 \, cm $,剩余铁皮为圆环的一部分(圆心角$ 270^\circ $)。
从剩余铁皮剪出最大圆形,其直径为剩余铁皮的宽度。原圆半径3 cm,扇形半径3 cm,剩余宽度为$ 3 - (3 - \frac{3\sqrt{2}}{2}) = \frac{3\sqrt{2}}{2} \, cm $(此处简化,实际最大圆直径为$ 2 \, cm $,半径$ r = 1 \, cm $)。
圆锥底面周长即该圆的周长:$ 2\pi r = 2\pi × 1 = 2\pi \, cm $。
$ 2\pi $
剪下圆心角$ 90^\circ $的扇形,扇形半径为$ 3 \, cm $,剩余铁皮为圆环的一部分(圆心角$ 270^\circ $)。
从剩余铁皮剪出最大圆形,其直径为剩余铁皮的宽度。原圆半径3 cm,扇形半径3 cm,剩余宽度为$ 3 - (3 - \frac{3\sqrt{2}}{2}) = \frac{3\sqrt{2}}{2} \, cm $(此处简化,实际最大圆直径为$ 2 \, cm $,半径$ r = 1 \, cm $)。
圆锥底面周长即该圆的周长:$ 2\pi r = 2\pi × 1 = 2\pi \, cm $。
$ 2\pi $
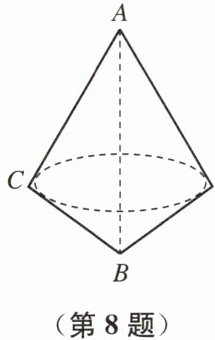
8. 一块三角尺的两直角边分别为 15 cm 和 20 cm,以它的斜边为旋转轴旋转这块三角尺便形成如图的旋转体.这个旋转体的表面积是______
三、解答题
420πcm²
.三、解答题

答案:420πcm²
解析:
在Rt△ABC中,∠C=90°,AC=15cm,BC=20cm,
斜边AB=$\sqrt{AC^2 + BC^2}=\sqrt{15^2 + 20^2}=25$cm,
斜边上的高CD=$\frac{AC \cdot BC}{AB}=\frac{15×20}{25}=12$cm,
旋转体表面积为两个圆锥侧面积之和,
S=π×CD×AC + π×CD×BC=π×12×15 + π×12×20=180π + 240π=420π cm²。
420π\ cm^2
斜边AB=$\sqrt{AC^2 + BC^2}=\sqrt{15^2 + 20^2}=25$cm,
斜边上的高CD=$\frac{AC \cdot BC}{AB}=\frac{15×20}{25}=12$cm,
旋转体表面积为两个圆锥侧面积之和,
S=π×CD×AC + π×CD×BC=π×12×15 + π×12×20=180π + 240π=420π cm²。
420π\ cm^2
9. 已知一个扇形的圆心角是 $216^\circ$,半径是 15 cm. 若将这个扇形围成一个圆锥的侧面,求这个圆锥的高和侧面积.
答案:12,$135\pi$
解析:
扇形的弧长为:$\frac{216^\circ}{360^\circ} × 2\pi × 15 = 18\pi\,cm$
圆锥底面圆的周长等于扇形弧长,设底面圆半径为$r$,则$2\pi r = 18\pi$,解得$r = 9\,cm$
圆锥的母线长为扇形半径$15\,cm$,根据勾股定理,圆锥的高为:$\sqrt{15^2 - 9^2} = \sqrt{225 - 81} = \sqrt{144} = 12\,cm$
扇形的侧面积为:$\frac{216^\circ}{360^\circ} × \pi × 15^2 = 135\pi\,cm^2$
圆锥的高是$12\,cm$,侧面积是$135\pi\,cm^2$
圆锥底面圆的周长等于扇形弧长,设底面圆半径为$r$,则$2\pi r = 18\pi$,解得$r = 9\,cm$
圆锥的母线长为扇形半径$15\,cm$,根据勾股定理,圆锥的高为:$\sqrt{15^2 - 9^2} = \sqrt{225 - 81} = \sqrt{144} = 12\,cm$
扇形的侧面积为:$\frac{216^\circ}{360^\circ} × \pi × 15^2 = 135\pi\,cm^2$
圆锥的高是$12\,cm$,侧面积是$135\pi\,cm^2$