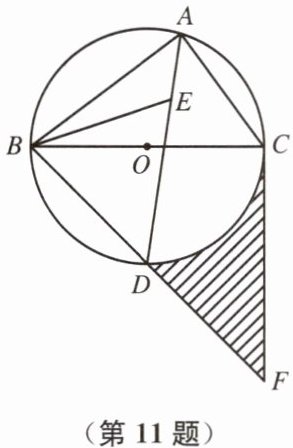
11. 如图,$\odot O是\triangle ABC$的外接圆,$BC为\odot O$的直径,$E为\triangle ABC$的内心,连接$AE并延长交\odot O于点D$,连接$BE$.
(1)求证:$DB= DE$;
(2)若过点$C的切线与BD的延长线交于点F$,已知$DE= 3\sqrt{2}$,求$\overset{\frown}{DC}$、线段$DF$、$CF$围成的阴影部分面积.
(1)求证:$DB= DE$;
(2)若过点$C的切线与BD的延长线交于点F$,已知$DE= 3\sqrt{2}$,求$\overset{\frown}{DC}$、线段$DF$、$CF$围成的阴影部分面积.

答案:
证明:( 1 ) :∵E是△ABC的内心.
∴∠BAE=∠CAE,∠EBA=∠EBC,
∵∠BED=∠BAE+∠ABE,
∠DBE=∠EBC+∠DBC,∠DBC=∠EAC,
∴∠DBE=∠DEB,
∴DB=DE.
解:( 2 ) 连接CD、OD
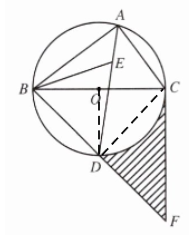
∴∠BAD=∠DAC,
∴$\overgroup{BD}=\overgroup{CD},$
∴BD=CD,
∵BC是直径,
∴∠BDC=90°,
∴∠DBC=∠DCB=45°,
∵FC是切线,
∴∠BCF=90°,∴∠DCF=45°,
∴△CDF是等腰直角三角形,
∵$DE=DB=3\sqrt{2},$
∴OD=OC=3,$DF=CD=BD=3\sqrt{2},$
∴S_阴=S_{△CDF}-( S_{扇形OCD}-S_{△OCD} )
$=\frac {1}{2}×3\sqrt{2}×3\sqrt{2}-$
$(\frac {90×\pi ×3^2}{360}-\frac {1}{2}×3×3) $
$=\frac {27}{2}-\frac {9\pi}{4} $
证明:( 1 ) :∵E是△ABC的内心.
∴∠BAE=∠CAE,∠EBA=∠EBC,
∵∠BED=∠BAE+∠ABE,
∠DBE=∠EBC+∠DBC,∠DBC=∠EAC,
∴∠DBE=∠DEB,
∴DB=DE.
解:( 2 ) 连接CD、OD

∴∠BAD=∠DAC,
∴$\overgroup{BD}=\overgroup{CD},$
∴BD=CD,
∵BC是直径,
∴∠BDC=90°,
∴∠DBC=∠DCB=45°,
∵FC是切线,
∴∠BCF=90°,∴∠DCF=45°,
∴△CDF是等腰直角三角形,
∵$DE=DB=3\sqrt{2},$
∴OD=OC=3,$DF=CD=BD=3\sqrt{2},$
∴S_阴=S_{△CDF}-( S_{扇形OCD}-S_{△OCD} )
$=\frac {1}{2}×3\sqrt{2}×3\sqrt{2}-$
$(\frac {90×\pi ×3^2}{360}-\frac {1}{2}×3×3) $
$=\frac {27}{2}-\frac {9\pi}{4} $
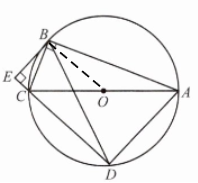
12. 如图,$\odot O是Rt\triangle ABC$的外接圆,$\angle ABC= 90^{\circ}$,弦$BD= BA$,$BE\perp DC$,并且交$DC的延长线于点E$.
(1)求证:$\angle BCA= \angle BAD$;
(2)求证:$BE是\odot O$的切线.

(1)求证:$\angle BCA= \angle BAD$;
(2)求证:$BE是\odot O$的切线.

答案:
证明:( 1 ) ∵∠BCA、∠BDA都是$\overset{\LARGE{ \frown}}{AB}$所对的圆周角
∴∠BCA=∠BDA
∵BD=BA
∴BAD=∠BDA
∴∠BCA=∠BAD
( 2 ) 连接OB,
∵OB=OC,BD=BA
∴∠BCA=∠CBO,∠BAD=∠BDA
∴∠BOC=180°-2∠BCA,∠ABD=180°-2∠BAD
∵∠BCA=∠BAD
∴∠BOC=∠ABD
∵∠ABD、∠ACD都是$\overgroup{AD}$所对的圆周角
∴∠ABD=∠ACD=∠BOC
∴CD//OB
∵BE⊥CD
∴BE⊥OB
∴BE是$\odot O$的切线
证明:( 1 ) ∵∠BCA、∠BDA都是$\overset{\LARGE{ \frown}}{AB}$所对的圆周角
∴∠BCA=∠BDA
∵BD=BA
∴BAD=∠BDA
∴∠BCA=∠BAD
( 2 ) 连接OB,
∵OB=OC,BD=BA
∴∠BCA=∠CBO,∠BAD=∠BDA
∴∠BOC=180°-2∠BCA,∠ABD=180°-2∠BAD
∵∠BCA=∠BAD
∴∠BOC=∠ABD
∵∠ABD、∠ACD都是$\overgroup{AD}$所对的圆周角
∴∠ABD=∠ACD=∠BOC
∴CD//OB
∵BE⊥CD
∴BE⊥OB
∴BE是$\odot O$的切线
