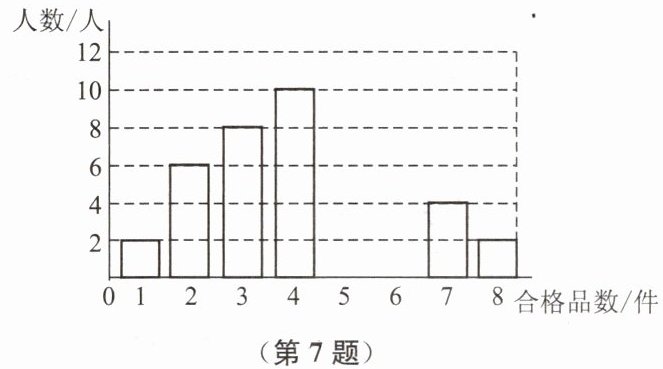
7. 某厂为了解工人在单位时间内加工同一种零件的技能水平,随机抽取了50名工人加工的零件进行检测,统计出他们各自加工的合格品数为1~8件,现提供条形统计图的部分信息如图,请解答下列问题:
(1)根据条形统计图,求这50名工人加工出的合格品数的中位数;
(2)写出这50名工人加工出的合格品数的众数的可能取值.
(1)根据条形统计图,求这50名工人加工出的合格品数的中位数;
(2)写出这50名工人加工出的合格品数的众数的可能取值.

答案:
解:(1)把这50名工人加工出的合格品数从小到大排列,第25、26个数都为4.
∴中位数是4件
(2)这50名工人加工出的合格品数的众数可能取4件、5件或6件.
解:(1)把这50名工人加工出的合格品数从小到大排列,第25、26个数都为4.
∴中位数是4件
(2)这50名工人加工出的合格品数的众数可能取4件、5件或6件.
8. 某汽车评测机构对市面上多款新能源汽车从0加速到100 km/h的时间和满电续航里程进行了性能评测,评测结果如图所示,每个点都对应一款新能源汽车的评测数据.已知车速由0加速到100 km/h的加速时间的中位数是m s,满电续航里程的中位数是n km,相应的直线将平面分成了①、②、③、④四个区域.欲将最新上市的两款新能源汽车的评测数据对应的点绘制到平面内,若已知绘制以后以上两组数据的中位数均保持不变,则这两个点可能分别落在(
A.区域①、②
B.区域①、③
C.区域①、④
D.区域③、④
B
)A.区域①、②
B.区域①、③
C.区域①、④
D.区域③、④
答案:B
解析:
设原数据中加速时间的个数为$k$,续航里程的个数为$k$。
原加速时间中位数$m$,新增两个点后,若两点加速时间均$\leq m$,则中位数可能变小;均$\geq m$,可能变大;一$\leq m$一$\geq m$,中位数不变。
原续航里程中位数$n$,新增两个点后,若两点续航里程均$\leq n$,中位数可能变小;均$\geq n$,可能变大;一$\leq n$一$\geq n$,中位数不变。
区域①:加速时间$< m$,续航里程$< n$;区域②:加速时间$< m$,续航里程$> n$;区域③:加速时间$> m$,续航里程$> n$;区域④:加速时间$> m$,续航里程$< n$。
选项B中区域①($<m,<n$)和区域③($>m,>n$),满足加速时间一$\leq m$一$\geq m$,续航里程一$\leq n$一$\geq n$,中位数均不变。
B
原加速时间中位数$m$,新增两个点后,若两点加速时间均$\leq m$,则中位数可能变小;均$\geq m$,可能变大;一$\leq m$一$\geq m$,中位数不变。
原续航里程中位数$n$,新增两个点后,若两点续航里程均$\leq n$,中位数可能变小;均$\geq n$,可能变大;一$\leq n$一$\geq n$,中位数不变。
区域①:加速时间$< m$,续航里程$< n$;区域②:加速时间$< m$,续航里程$> n$;区域③:加速时间$> m$,续航里程$> n$;区域④:加速时间$> m$,续航里程$< n$。
选项B中区域①($<m,<n$)和区域③($>m,>n$),满足加速时间一$\leq m$一$\geq m$,续航里程一$\leq n$一$\geq n$,中位数均不变。
B