2. 数据2,1,3,1,7,3的中位数是(
A.1
B.2
C.2.5
D.3
C
)A.1
B.2
C.2.5
D.3
答案:C
解析:
将数据按从小到大排列:1,1,2,3,3,7
数据个数为6,是偶数,中位数为中间两个数的平均数,即第3个数和第4个数的平均数
第3个数是2,第4个数是3
中位数为$\frac{2+3}{2}=2.5$
C.
数据个数为6,是偶数,中位数为中间两个数的平均数,即第3个数和第4个数的平均数
第3个数是2,第4个数是3
中位数为$\frac{2+3}{2}=2.5$
C.
3. 某8种食品所含的热量分别为(单位:卡路里)120,134,120,119,126,120,118,124.这组食品热量的众数为
120
卡路里.答案:120
4. 某班体育委员对本班同学一周锻炼时间(单位:h)进行了统计,绘制了如图所示的折线统计图,则该班学生一周锻炼时间的中位数是
11
h.答案:11
5. 如图是七(1)班40名同学一周家务劳动时间的频数分布直方图,设这组数据的中位数为m h,则m
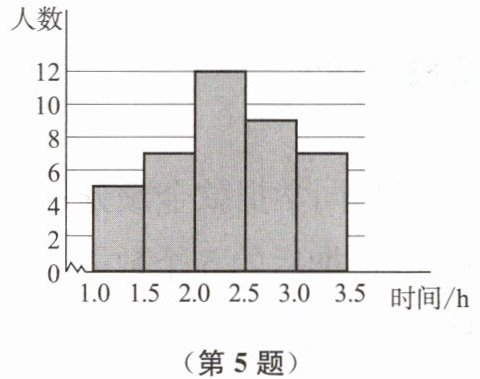
<
2.6(填“>”“=”或“<”).
答案:<
解析:
由频数分布直方图可知,各时间段人数依次为5,7,12,9,7。总人数40,中位数是第20和21个数据的平均数。前两组累计人数5+7=12,前三组累计5+7+12=24,故第20和21个数据在2.0~2.5小时组,该组数据均小于2.5,所以中位数m<2.5<2.6。
<
<
6. 某校为了普及“载人潜水器”知识,从该校1200名学生中随机抽取了200名学生参加“载人潜水器”知识测试,并将成绩整理绘制成如下不完整的统计表:

(1)求a的值;
(2)这200名学生成绩的中位数在哪个组别?

(1)求a的值;
(2)这200名学生成绩的中位数在哪个组别?
答案:1. (1)
解:因为各百分比之和为$100\%$(即$1$),所以$a = 1-(5\% + 15\%+35\% + 25\%)$
先计算括号内的值:$5\% + 15\%+35\% + 25\%=(5 + 15+35 + 25)\%$
根据加法运算$5 + 15+35 + 25=(5 + 15)+(35 + 25)=20 + 60 = 80\%$。
则$a=1 - 80\%=20\%$。
2. (2)
解:$A$组人数:$n_{A}=200×5\% = 10$人;
$B$组人数:$n_{B}=200×15\% = 30$人;
$C$组人数:$n_{C}=200×20\% = 40$人;
$D$组人数:$n_{D}=200×35\% = 70$人;
$E$组人数:$n_{E}=200×25\% = 50$人。
因为一共有$n = 200$个数据,中位数是第$\frac{n}{2}=100$个和第$\frac{n}{2}+1 = 101$个数据的平均数。
$A$组与$B$组人数之和为$n_{A}+n_{B}=10 + 30=40$人;
$A$组、$B$组与$C$组人数之和为$n_{A}+n_{B}+n_{C}=10 + 30+40 = 80$人;
$A$组、$B$组、$C$组与$D$组人数之和为$n_{A}+n_{B}+n_{C}+n_{D}=10 + 30+40 + 70=150$人。
由于$80\lt100\lt150$,所以这$200$名学生成绩的中位数在$D$组。
综上,(1)$a = 20\%$;(2)中位数在$D$组。
解:因为各百分比之和为$100\%$(即$1$),所以$a = 1-(5\% + 15\%+35\% + 25\%)$
先计算括号内的值:$5\% + 15\%+35\% + 25\%=(5 + 15+35 + 25)\%$
根据加法运算$5 + 15+35 + 25=(5 + 15)+(35 + 25)=20 + 60 = 80\%$。
则$a=1 - 80\%=20\%$。
2. (2)
解:$A$组人数:$n_{A}=200×5\% = 10$人;
$B$组人数:$n_{B}=200×15\% = 30$人;
$C$组人数:$n_{C}=200×20\% = 40$人;
$D$组人数:$n_{D}=200×35\% = 70$人;
$E$组人数:$n_{E}=200×25\% = 50$人。
因为一共有$n = 200$个数据,中位数是第$\frac{n}{2}=100$个和第$\frac{n}{2}+1 = 101$个数据的平均数。
$A$组与$B$组人数之和为$n_{A}+n_{B}=10 + 30=40$人;
$A$组、$B$组与$C$组人数之和为$n_{A}+n_{B}+n_{C}=10 + 30+40 = 80$人;
$A$组、$B$组、$C$组与$D$组人数之和为$n_{A}+n_{B}+n_{C}+n_{D}=10 + 30+40 + 70=150$人。
由于$80\lt100\lt150$,所以这$200$名学生成绩的中位数在$D$组。
综上,(1)$a = 20\%$;(2)中位数在$D$组。