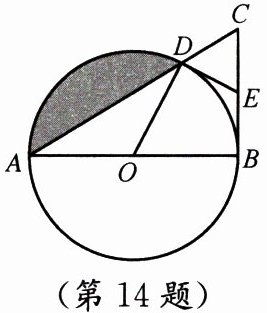
14. (10 分)如图,在 $\triangle ABC$ 中,$\angle ABC = 90^{\circ}$,以 $AB$ 为直径的 $\odot O$ 交 $AC$ 于点 $D$,$E$ 为 $BC$ 的中点,连接 $OD、DE$.
(1) 求证:$OD \perp DE$;
(2) 若 $\angle BAC = 30^{\circ}$,$AB = 12$,求阴影部分的面积.
(1) 求证:$OD \perp DE$;
(2) 若 $\angle BAC = 30^{\circ}$,$AB = 12$,求阴影部分的面积.

答案:(1) 见证明;(2) $12π$。
解析:
(1) 证明:
∵AB为⊙O直径,∴O为AB中点,OA=OD,∠ADB=90°(直径所对圆周角为直角)。
∴∠OAD=∠ODA。设∠OAD=α,则∠ODA=α。
∵∠ABC=90°,∴∠ACB=90°-α。
∵E为BC中点,∠BDC=90°(∠ADB=90°),∴DE=BE=CE(直角三角形斜边中线等于斜边一半)。
∴∠EBD=∠EDB。
∵∠ABD=90°-α(△ABD中∠ADB=90°),∴∠DBC=∠ABC-∠ABD=α,即∠EBD=α,∴∠EDB=α。
∵A、D、C共线,∴∠ODC=180°-∠ODA=180°-α。
∠EDC=∠ACB=90°-α(DE=CE)。
∴∠ODE=∠ODC-∠EDC=(180°-α)-(90°-α)=90°。
∴OD⊥DE。
(2) 解:
∵∠BAC=30°,AB=12,∴⊙O半径OA=OD=6。
∵OA=OD,∴∠OAD=∠ODA=30°,∠AOD=180°-30°-30°=120°。
阴影部分为扇形OAD,面积S= $\frac{120}{360}π×6^2=12π$。
∵AB为⊙O直径,∴O为AB中点,OA=OD,∠ADB=90°(直径所对圆周角为直角)。
∴∠OAD=∠ODA。设∠OAD=α,则∠ODA=α。
∵∠ABC=90°,∴∠ACB=90°-α。
∵E为BC中点,∠BDC=90°(∠ADB=90°),∴DE=BE=CE(直角三角形斜边中线等于斜边一半)。
∴∠EBD=∠EDB。
∵∠ABD=90°-α(△ABD中∠ADB=90°),∴∠DBC=∠ABC-∠ABD=α,即∠EBD=α,∴∠EDB=α。
∵A、D、C共线,∴∠ODC=180°-∠ODA=180°-α。
∠EDC=∠ACB=90°-α(DE=CE)。
∴∠ODE=∠ODC-∠EDC=(180°-α)-(90°-α)=90°。
∴OD⊥DE。
(2) 解:
∵∠BAC=30°,AB=12,∴⊙O半径OA=OD=6。
∵OA=OD,∴∠OAD=∠ODA=30°,∠AOD=180°-30°-30°=120°。
阴影部分为扇形OAD,面积S= $\frac{120}{360}π×6^2=12π$。
15. (10 分)如图,$\odot O$ 的直径 $AB$ 为 10 cm,弦 $BC$ 为 6 cm,$D、E$ 分别是 $\angle ACB$ 的平分线与 $\odot O、AB$ 的交点,$P$ 为 $AB$ 延长线上一点,且 $PC = PE$.
(1) 求 $AC、AD$ 的长;
(2) 试判断直线 $PC$ 与 $\odot O$ 的位置关系,并说明理由.

(1) 求 $AC、AD$ 的长;
(2) 试判断直线 $PC$ 与 $\odot O$ 的位置关系,并说明理由.

答案:(1)
因为$AB$为$\odot O$直径,所以$\angle ACB = 90^{\circ}$。
在$Rt\triangle ABC$中,$AB = 10cm$,$BC = 6cm$,根据勾股定理$AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{10^{2}-6^{2}} = 8cm$。
连接$BD$,因为$AB$是直径,所以$\angle ADB = 90^{\circ}$。
$D$、$E$分别是$\angle ACB$的平分线与$\odot O$、$AB$的交点,所以$\angle ACD=\angle BCD = 45^{\circ}$,根据同弧所对的圆周角相等可得$\angle DAB=\angle BCD = 45^{\circ}$。
在$Rt\triangle ABD$中,$\angle DAB = 45^{\circ}$,$\angle ABD = 45^{\circ}$,则$AD = BD$。
由勾股定理$AB^{2}=AD^{2}+BD^{2}$,即$10^{2}=2AD^{2}$,解得$AD = 5\sqrt{2}cm$。
(2)
连接$OC$。
因为$OC = OA$,所以$\angle OAC=\angle OCA$。
由(1)知$\angle CAD = 45^{\circ}$,所以$\angle OAC=\angle OCA = 45^{\circ}-\angle CAE$(设$\angle CAE$为$\alpha$),则$\angle COP = 2\angle CAE$(同弧所对的圆心角是圆周角的两倍)。
在$\triangle ACE$和$\triangle PCE$中,$PC = PE$,所以$\angle PEC=\angle PCE$。
又因为$\angle PEC=\angle CAE+\angle ACE=\angle CAE + 45^{\circ}$,$\angle PCE=\angle PCO+\angle OCA$。
$\angle OCA=\angle OAC$,$\angle PCO=\angle PEC-\angle OCA=\angle CAE + 45^{\circ}-\angle OCA$。
$\angle OCP=\angle PCO+\angle OCA=\angle CAE + 45^{\circ}$。
$\angle OAC+\angle CAE+\angle ACO = 90^{\circ}$,$\angle OCA=\angle OAC$,所以$\angle OCP = 90^{\circ}$,即$OC\perp PC$。
因为$OC$是$\odot O$的半径,所以直线$PC$与$\odot O$相切。
综上,(1)$AC = 8cm$,$AD = 5\sqrt{2}cm$;(2)直线$PC$与$\odot O$相切。
因为$AB$为$\odot O$直径,所以$\angle ACB = 90^{\circ}$。
在$Rt\triangle ABC$中,$AB = 10cm$,$BC = 6cm$,根据勾股定理$AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{10^{2}-6^{2}} = 8cm$。
连接$BD$,因为$AB$是直径,所以$\angle ADB = 90^{\circ}$。
$D$、$E$分别是$\angle ACB$的平分线与$\odot O$、$AB$的交点,所以$\angle ACD=\angle BCD = 45^{\circ}$,根据同弧所对的圆周角相等可得$\angle DAB=\angle BCD = 45^{\circ}$。
在$Rt\triangle ABD$中,$\angle DAB = 45^{\circ}$,$\angle ABD = 45^{\circ}$,则$AD = BD$。
由勾股定理$AB^{2}=AD^{2}+BD^{2}$,即$10^{2}=2AD^{2}$,解得$AD = 5\sqrt{2}cm$。
(2)
连接$OC$。
因为$OC = OA$,所以$\angle OAC=\angle OCA$。
由(1)知$\angle CAD = 45^{\circ}$,所以$\angle OAC=\angle OCA = 45^{\circ}-\angle CAE$(设$\angle CAE$为$\alpha$),则$\angle COP = 2\angle CAE$(同弧所对的圆心角是圆周角的两倍)。
在$\triangle ACE$和$\triangle PCE$中,$PC = PE$,所以$\angle PEC=\angle PCE$。
又因为$\angle PEC=\angle CAE+\angle ACE=\angle CAE + 45^{\circ}$,$\angle PCE=\angle PCO+\angle OCA$。
$\angle OCA=\angle OAC$,$\angle PCO=\angle PEC-\angle OCA=\angle CAE + 45^{\circ}-\angle OCA$。
$\angle OCP=\angle PCO+\angle OCA=\angle CAE + 45^{\circ}$。
$\angle OAC+\angle CAE+\angle ACO = 90^{\circ}$,$\angle OCA=\angle OAC$,所以$\angle OCP = 90^{\circ}$,即$OC\perp PC$。
因为$OC$是$\odot O$的半径,所以直线$PC$与$\odot O$相切。
综上,(1)$AC = 8cm$,$AD = 5\sqrt{2}cm$;(2)直线$PC$与$\odot O$相切。