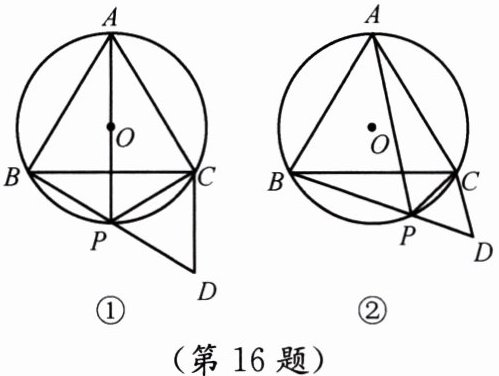
16. (10 分)如图,等边三角形 $ABC$ 内接于 $\odot O$,$P$ 是劣弧 $BC$ 上的一点(端点除外),延长 $BP$ 至点 $D$,使 $BD = AP$,连接 $CD$.
(1) 若 $AP$ 过圆心 $O$(图①),请判断 $\triangle PDC$ 是什么三角形;
(2) 若 $AP$ 不过圆心 $O$(图②),请判断 $\triangle PDC$ 是什么三角形,并说明理由.
(1) 若 $AP$ 过圆心 $O$(图①),请判断 $\triangle PDC$ 是什么三角形;
(2) 若 $AP$ 不过圆心 $O$(图②),请判断 $\triangle PDC$ 是什么三角形,并说明理由.

答案:(1) △PDC是等边三角形。
理由:
∵△ABC是等边三角形,∴AB=BC,∠BAC=60°。
∵AP过圆心O,∴AP平分∠BAC,∠BAP=30°。
∵点P在劣弧BC上,∴∠BCP=∠BAP=30°(同弧BP所对圆周角相等)。
∵BD=AP,AB=BC,∠BAP=∠CBD=30°(可证弧BP=弧PC=60°,得∠CBD=30°),
∴△ABP≌△CBD(SAS),∴BP=CD,∠ABP=∠BCD=30°。
∴∠PCD=∠BCD+∠BCP=30°+30°=60°,又CD=PC(等弧对等弦),
∴△PDC是等边三角形。
(2) △PDC是等边三角形。
理由:
∵△ABC是等边三角形,∴AB=BC,∠BAC=60°。
∵点P在劣弧BC上,∴∠BAP=∠BCP(同弧BP所对圆周角相等),∠PAC=∠PBC(同弧PC所对圆周角相等)。
∵BD=AP,AB=BC,∠PAC=∠DBC,∴△APC≌△BDC(SAS),∴PC=DC。
∵∠ACB=60°,∠ACP=∠BCD(全等三角形对应角相等),
∴∠PCD=∠ACB=60°(∠PCD=∠BCD+∠BCP=∠ACP+∠BCP=∠ACB)。
∵PC=DC,∠PCD=60°,∴△PDC是等边三角形。
理由:
∵△ABC是等边三角形,∴AB=BC,∠BAC=60°。
∵AP过圆心O,∴AP平分∠BAC,∠BAP=30°。
∵点P在劣弧BC上,∴∠BCP=∠BAP=30°(同弧BP所对圆周角相等)。
∵BD=AP,AB=BC,∠BAP=∠CBD=30°(可证弧BP=弧PC=60°,得∠CBD=30°),
∴△ABP≌△CBD(SAS),∴BP=CD,∠ABP=∠BCD=30°。
∴∠PCD=∠BCD+∠BCP=30°+30°=60°,又CD=PC(等弧对等弦),
∴△PDC是等边三角形。
(2) △PDC是等边三角形。
理由:
∵△ABC是等边三角形,∴AB=BC,∠BAC=60°。
∵点P在劣弧BC上,∴∠BAP=∠BCP(同弧BP所对圆周角相等),∠PAC=∠PBC(同弧PC所对圆周角相等)。
∵BD=AP,AB=BC,∠PAC=∠DBC,∴△APC≌△BDC(SAS),∴PC=DC。
∵∠ACB=60°,∠ACP=∠BCD(全等三角形对应角相等),
∴∠PCD=∠ACB=60°(∠PCD=∠BCD+∠BCP=∠ACP+∠BCP=∠ACB)。
∵PC=DC,∠PCD=60°,∴△PDC是等边三角形。
17. (12 分)如图,$PA、PB$ 分别与 $\odot O$ 相切于点 $A、B$,点 $M$ 在 $PB$ 上,且 $OM // AP$,$MN \perp AP$,垂足为 $N$.
(1) 求证:$OM = AN$;
(2) 已知 $\odot O$ 的半径 $R = 3$,$PA = 9$,求 $OM$ 的长.

(1) 求证:$OM = AN$;
(2) 已知 $\odot O$ 的半径 $R = 3$,$PA = 9$,求 $OM$ 的长.

答案:
(1) 见证明过程;
(2) 5。
(1) 见证明过程;
(2) 5。
解析:
(1) 证明:
∵PA是⊙O的切线,
∴OA⊥PA(切线垂直于经过切点的半径),即∠OAP=90°。
∵MN⊥AP,
∴∠MNP=90°,
∴OA//MN(垂直于同一直线的两直线平行)。
∵OM//AP(已知),
∴四边形OANM是平行四边形(两组对边分别平行的四边形是平行四边形)。
∴OM=AN(平行四边形对边相等)。
(2) 解:
设OM=AN=x,
∵PA=9,
∴PN=PA-AN=9-x。
∵四边形OANM是平行四边形,
∴MN=OA=R=3(平行四边形对边相等)。
∵PB是⊙O的切线,
∴PB=PA=9(切线长定理),OB⊥PB(切线垂直于经过切点的半径),即∠OBP=90°。
设BM=PB-PM=9-PM,在Rt△OBM中,OB=3,OM=x,由勾股定理得:BM²=OM²-OB²=x²-9,
∴BM=√(x²-9),则PM=PB-BM=9-√(x²-9)。
在Rt△PMN中,MN=3,PN=9-x,PM=9-√(x²-9),由勾股定理得:PM²=PN²+MN²,即(9-√(x²-9))²=(9-x)²+3²。
展开并化简:81-18√(x²-9)+x²-9=81-18x+x²+9,
整理得:-18√(x²-9)=-18x+18,即√(x²-9)=x-1。
两边平方:x²-9=x²-2x+1,解得2x=10,x=5。
∴OM=5。