17. (14分)某中学举行校园歌手大赛,初中部、高中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,选手的决赛成绩如图所示.
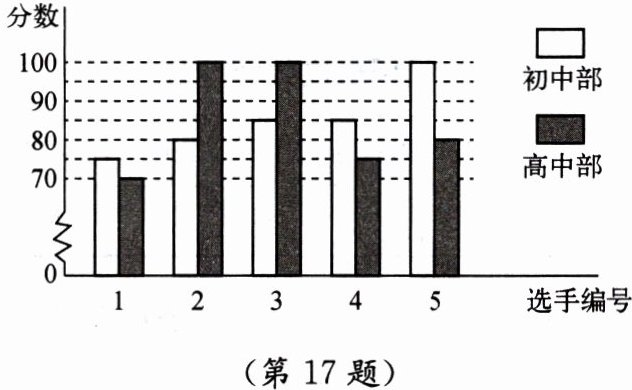
(1)根据图示填写下表:
| 代表队 | 平均数 | 中位数 | 众数 |
| 初中部 | | 85 | |
| 高中部 | 85 | | 100 |

(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差,并判断哪一个代表队选手的成绩较为稳定.

(1)根据图示填写下表:
| 代表队 | 平均数 | 中位数 | 众数 |
| 初中部 | | 85 | |
| 高中部 | 85 | | 100 |

(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差,并判断哪一个代表队选手的成绩较为稳定.
答案:(1)
| 代表队 | 平均数 | 中位数 | 众数 |
|--------|--------|--------|------|
| 初中部 | 85 | 85 | 85 |
| 高中部 | 85 | 80 | 100 |
(2) 两队成绩的平均数相同,均为85分。初中部成绩的中位数为85分,高于高中部的80分,说明初中部成绩的中间水平更高,因此初中部决赛成绩较好。
(3) 初中部成绩:80,85,85,85,90,平均数$\bar{x}_1=85$。
方差$S_1^2=\frac{1}{5}[(80-85)^2+(85-85)^2+(85-85)^2+(85-85)^2+(90-85)^2]=\frac{1}{5}(25+0+0+0+25)=10$。
高中部成绩:70,75,80,100,100,平均数$\bar{x}_2=85$。
方差$S_2^2=\frac{1}{5}[(70-85)^2+(75-85)^2+(80-85)^2+(100-85)^2+(100-85)^2]=\frac{1}{5}(225+100+25+225+225)=160$。
因为$10<160$,所以初中代表队选手的成绩较为稳定。
| 代表队 | 平均数 | 中位数 | 众数 |
|--------|--------|--------|------|
| 初中部 | 85 | 85 | 85 |
| 高中部 | 85 | 80 | 100 |
(2) 两队成绩的平均数相同,均为85分。初中部成绩的中位数为85分,高于高中部的80分,说明初中部成绩的中间水平更高,因此初中部决赛成绩较好。
(3) 初中部成绩:80,85,85,85,90,平均数$\bar{x}_1=85$。
方差$S_1^2=\frac{1}{5}[(80-85)^2+(85-85)^2+(85-85)^2+(85-85)^2+(90-85)^2]=\frac{1}{5}(25+0+0+0+25)=10$。
高中部成绩:70,75,80,100,100,平均数$\bar{x}_2=85$。
方差$S_2^2=\frac{1}{5}[(70-85)^2+(75-85)^2+(80-85)^2+(100-85)^2+(100-85)^2]=\frac{1}{5}(225+100+25+225+225)=160$。
因为$10<160$,所以初中代表队选手的成绩较为稳定。