1. 方程 $ x^{2}-2x = 0 $ 的解是(
A.$ x = 2 $
B.$ x = 0 $
C.$ x_{1}= 0,x_{2}= -2 $
D.$ x_{1}= 0,x_{2}= 2 $
D
)A.$ x = 2 $
B.$ x = 0 $
C.$ x_{1}= 0,x_{2}= -2 $
D.$ x_{1}= 0,x_{2}= 2 $
答案:D
解析:
方程左边分解因式得$x(x - 2) = 0$,则$x = 0$或$x - 2 = 0$,解得$x_1 = 0$,$x_2 = 2$。
2. 下列说法中,正确的是(
A.三点可以确定一个圆
B.半圆(或直径)所对的圆周角是直角
C.相等的圆心角所对的弧相等
D.过圆上一点的直线与圆相切
B
)A.三点可以确定一个圆
B.半圆(或直径)所对的圆周角是直角
C.相等的圆心角所对的弧相等
D.过圆上一点的直线与圆相切
答案:B
解析:
A.不在同一直线上的三点确定一个圆,故A错误;B.半圆(或直径)所对的圆周角是直角,正确;C.在同圆或等圆中,相等的圆心角所对的弧相等,故C错误;D.过圆上一点且垂直于该点半径的直线与圆相切,故D错误。
3. 已知 $ x = 1 $ 是关于 $ x $ 的方程 $ x^{2}+ax + 2 = 0 $ 的一个根,则方程的另一个根为(
A.$ -2 $
B.$ 2 $
C.$ -3 $
D.$ 3 $
B
)A.$ -2 $
B.$ 2 $
C.$ -3 $
D.$ 3 $
答案:B
解析:
设方程的另一个根为$x_2$,由韦达定理得$1× x_2 = 2$,解得$x_2 = 2$。
4. 如图,点 $ A、B、C $ 在 $ \odot O $ 上,且 $ \angle AOB = 80^{\circ} $,则 $ \angle ACB $ 等于(
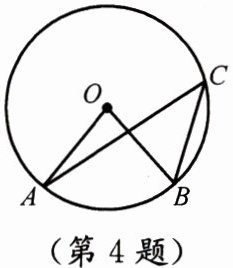
A.$ 100^{\circ} $
B.$ 80^{\circ} $
C.$ 50^{\circ} $
D.$ 40^{\circ} $
D
) 
A.$ 100^{\circ} $
B.$ 80^{\circ} $
C.$ 50^{\circ} $
D.$ 40^{\circ} $
答案:D
解析:
根据圆周角定理,同弧所对的圆周角等于圆心角的一半。
已知$\angle AOB$是圆心角,$\angle ACB$是圆周角,且它们所对的弧都是$\overset{\frown}{AB}$。
所以$\angle ACB=\frac{1}{2}\angle AOB$。
因为$\angle AOB = 80^{\circ}$,则$\angle ACB=\frac{1}{2}×80^{\circ}=40^{\circ}$。
已知$\angle AOB$是圆心角,$\angle ACB$是圆周角,且它们所对的弧都是$\overset{\frown}{AB}$。
所以$\angle ACB=\frac{1}{2}\angle AOB$。
因为$\angle AOB = 80^{\circ}$,则$\angle ACB=\frac{1}{2}×80^{\circ}=40^{\circ}$。
5. 关于 $ x $ 的一元二次方程 $ kx^{2}-2x - 1 = 0 $ 有两个不相等的实数根,则 $ k $ 的取值范围是(
A.$ k > -1 $
B.$ k > -1 $ 且 $ k \neq 0 $
C.$ k < 1 $
D.$ k < 1 $ 且 $ k \neq 0 $
B
)A.$ k > -1 $
B.$ k > -1 $ 且 $ k \neq 0 $
C.$ k < 1 $
D.$ k < 1 $ 且 $ k \neq 0 $
答案:B
解析:
一元二次方程 $kx^2 - 2x - 1 = 0$ 的判别式为 $\Delta = b^2 - 4ac$,其中 $a = k$,$b = -2$,$c = -1$。
代入得 $\Delta = (-2)^2 - 4 \cdot k \cdot (-1) = 4 + 4k$。
因为方程有两个不相等的实数根,所以 $\Delta > 0$,即 $4 + 4k > 0$,解得 $k > -1$。
又因为方程是一元二次方程,所以 $k \neq 0$。
综上,$k$ 的取值范围是 $k > -1$ 且 $k \neq 0$。
代入得 $\Delta = (-2)^2 - 4 \cdot k \cdot (-1) = 4 + 4k$。
因为方程有两个不相等的实数根,所以 $\Delta > 0$,即 $4 + 4k > 0$,解得 $k > -1$。
又因为方程是一元二次方程,所以 $k \neq 0$。
综上,$k$ 的取值范围是 $k > -1$ 且 $k \neq 0$。
6. 已知关于 $ x $ 的方程 $ (a - 6)x^{2}-8x + 6 = 0 $ 有实数根,则整数 $ a $ 的最大值是(
A.$ 6 $
B.$ 7 $
C.$ 8 $
D.$ 9 $
C
)A.$ 6 $
B.$ 7 $
C.$ 8 $
D.$ 9 $
答案:C
解析:
方程有实数根,则需满足以下条件:
当$a - 6 = 0$(即$a = 6$)时,方程退化为一次方程$-8x + 6 = 0$,显然有实数根。
当$a - 6 \neq 0$(即$a \neq 6$)时,方程为二次方程,需满足判别式$\Delta \geq 0$。
判别式为:
$\Delta = (-8)^2 - 4 × (a - 6) × 6 = 64 - 24(a - 6) = 64 - 24a + 144 = 208 - 24a$,
要求$\Delta \geq 0$,即:
$208 - 24a \geq 0 \implies a \leq \frac{208}{24} = \frac{26}{3} \approx 8.67$,
因为$a$为整数且$a \neq 6$时,$a$的最大值为$8$。
综合两种情况,$a$的最大整数值为$8$。
当$a - 6 = 0$(即$a = 6$)时,方程退化为一次方程$-8x + 6 = 0$,显然有实数根。
当$a - 6 \neq 0$(即$a \neq 6$)时,方程为二次方程,需满足判别式$\Delta \geq 0$。
判别式为:
$\Delta = (-8)^2 - 4 × (a - 6) × 6 = 64 - 24(a - 6) = 64 - 24a + 144 = 208 - 24a$,
要求$\Delta \geq 0$,即:
$208 - 24a \geq 0 \implies a \leq \frac{208}{24} = \frac{26}{3} \approx 8.67$,
因为$a$为整数且$a \neq 6$时,$a$的最大值为$8$。
综合两种情况,$a$的最大整数值为$8$。
7. 如图, $ AB $ 是 $ \odot O $ 的直径, $ PA $ 是 $ \odot O $ 的切线,切点为 $ A,PO $ 交 $ \odot O $ 于点 $ C $,连接 $ BC $. 若 $ \angle P = 40^{\circ} $,则 $ \angle B $ 等于(

A.$ 20^{\circ} $
B.$ 25^{\circ} $
C.$ 30^{\circ} $
D.$ 40^{\circ} $
B
)
A.$ 20^{\circ} $
B.$ 25^{\circ} $
C.$ 30^{\circ} $
D.$ 40^{\circ} $
答案:B
解析:
1. 因为$PA$是$\odot O$的切线,根据切线的性质可知$OA\perp PA$,所以$\angle OAP = 90^{\circ}$。
2. 已知$\angle P = 40^{\circ}$,在$\triangle OAP$中,根据三角形内角和为$180^{\circ}$,可得$\angle AOP=180^{\circ}-\angle OAP - \angle P=180^{\circ}-90^{\circ}-40^{\circ}=50^{\circ}$。
3. 因为$\angle AOP$是圆心角,$\angle B$是圆周角,且它们所对的弧都是$\overset{\frown}{AC}$,根据同弧所对的圆周角是圆心角的一半,所以$\angle B=\frac{1}{2}\angle AOP = 25^{\circ}$。
2. 已知$\angle P = 40^{\circ}$,在$\triangle OAP$中,根据三角形内角和为$180^{\circ}$,可得$\angle AOP=180^{\circ}-\angle OAP - \angle P=180^{\circ}-90^{\circ}-40^{\circ}=50^{\circ}$。
3. 因为$\angle AOP$是圆心角,$\angle B$是圆周角,且它们所对的弧都是$\overset{\frown}{AC}$,根据同弧所对的圆周角是圆心角的一半,所以$\angle B=\frac{1}{2}\angle AOP = 25^{\circ}$。
8. 某种商品价格受市场供需变化影响,1月份价格下降 $ 10\% $,经过2月份、3月份之后,又增长至原价,若2月份、3月份此商品价格的平均增长率为 $ x $,则 $ x $ 满足的方程是(
A.$ (1 + x)^{2}= \frac{11}{10} $
B.$ (1 + x)^{2}= \frac{10}{9} $
C.$ 1 + 2x= \frac{11}{10} $
D.$ 1 + 2x= \frac{10}{9} $
B
)A.$ (1 + x)^{2}= \frac{11}{10} $
B.$ (1 + x)^{2}= \frac{10}{9} $
C.$ 1 + 2x= \frac{11}{10} $
D.$ 1 + 2x= \frac{10}{9} $
答案:B
解析:
设原价为$a$元,1月份价格下降$10\%$后为$0.9a$元。
2、3月份价格以增长率$x$连续增长,最终恢复原价$a$元,则:
$0.9a(1 + x)^{2} = a$,
化简得:$(1 + x)^{2} = \frac{10}{9}$。
2、3月份价格以增长率$x$连续增长,最终恢复原价$a$元,则:
$0.9a(1 + x)^{2} = a$,
化简得:$(1 + x)^{2} = \frac{10}{9}$。
9. 一点和 $ \odot O $ 上的点的最近距离为 $ 4cm $,最远距离为 $ 9cm $,则 $ \odot O $ 的半径是
6.5或2.5
$ cm $.答案:6.5或2.5
解析:
当点在$\odot O$外时,半径$r=\frac{9-4}{2}=2.5$;当点在$\odot O$内时,半径$r=\frac{9+4}{2}=6.5$。
10. 如图,线段 $ AB $ 是 $ \odot O $ 的直径,弦 $ CD \perp AB,\angle CAB = 20^{\circ} $,则 $ \angle AOD = $

140°
.
答案:140°
解析:
连接OC,因为OA=OC,所以∠OCA=∠CAB=20°,则∠AOC=180°-20°×2=140°。因为AB是直径,CD⊥AB,所以AB垂直平分CD,故∠AOC=∠AOD=140°。