11. 已知 $ x = -1 $ 是关于 $ x $ 的方程 $ 2x^{2}+ax - a^{2}= 0 $ 的一个根,则 $ a = $
$-2$或$1$
.答案:$-2$或$1$(如果选项是单独对应填写形式则根据实际选项填写,这里按常规填答案)若为填空题形式则答案为$-2$或$1$。
解析:
将$x=-1$代入方程$2x^{2}+ax - a^{2}=0$中,得到$2×(-1)^{2}+a×(-1)-a^{2}=0$,即$2 - a - a^{2}=0$,等式两边同时乘以$-1$得$a^{2}+a - 2=0$,因式分解为$(a + 2)(a - 1)=0$,则$a + 2=0$或$a - 1=0$,解得$a=-2$或$a = 1$。
12. 已知关于 $ x $ 的一元二次方程 $ x^{2}-x - 3 = 0 $ 的两个实数根分别为 $ \alpha、\beta $,则 $ (\alpha + 3)(\beta + 3)= $
9
.答案:9
解析:
已知关于$x$的一元二次方程$x^{2}-x - 3 = 0$的两个实数根分别为$\alpha$、$\beta$,根据韦达定理可知$\alpha +\beta = 1$,$\alpha\beta = - 3$。
将$(\alpha + 3)(\beta + 3)$展开可得$\alpha\beta+3\alpha + 3\beta + 9=\alpha\beta + 3(\alpha + \beta)+9$。
把$\alpha +\beta = 1$,$\alpha\beta = - 3$代入上式可得:$-3+3×1 + 9=-3 + 3+9 = 9$。
将$(\alpha + 3)(\beta + 3)$展开可得$\alpha\beta+3\alpha + 3\beta + 9=\alpha\beta + 3(\alpha + \beta)+9$。
把$\alpha +\beta = 1$,$\alpha\beta = - 3$代入上式可得:$-3+3×1 + 9=-3 + 3+9 = 9$。
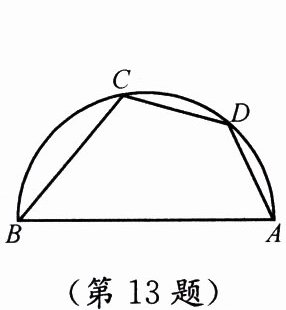
13. 如图, $ AB $ 是半圆的直径, $ D $ 是 $ \overset{\frown}{AC} $ 的中点, $ \angle ABC = 50^{\circ} $,则 $ \angle DAB = $
65°
.
答案:65°
解析:
连接AC,∵AB是半圆直径,∴∠ACB=90°(直径所对圆周角是直角)。在△ABC中,∠ABC=50°,∠ACB=90°,∴∠BAC=180°-90°-50°=40°。∠BAC所对弧为BC,故弧BC度数=2×40°=80°。∵AB为直径,弧AB=180°,∴弧AC=弧AB-弧BC=180°-80°=100°。∵D是弧AC中点,∴弧AD=弧DC=100°÷2=50°。∠DAC为弧DC所对圆周角,∴∠DAC=50°÷2=25°。∴∠DAB=∠DAC+∠BAC=25°+40°=65°。
14. 某药品经过两次降价,每瓶零售价由100元降为81元.已知两次降价的百分率相同,则降价的百分率为
10%
.答案:$10\%$
解析:
设每次降价的百分率为$x$,则第一次降价后的价格为$100(1 - x)$元,第二次降价后的价格为$100(1 - x)^2$元。
根据题意,有方程:$100(1 - x)^2 = 81$,
$(1 - x)^2 = 0.81$,
$1 - x = \pm 0.9$,
解得$x_1 = 0.1$,$x_2 = 1.9$(舍去,因为降价百分率不能超过$100\%$)。
所以降价的百分率为$10\%$。
根据题意,有方程:$100(1 - x)^2 = 81$,
$(1 - x)^2 = 0.81$,
$1 - x = \pm 0.9$,
解得$x_1 = 0.1$,$x_2 = 1.9$(舍去,因为降价百分率不能超过$100\%$)。
所以降价的百分率为$10\%$。
15. 如图, $ \odot O $ 的半径 $ OD $ 垂直于弦 $ AB $,垂足为 $ C $,连接 $ AO $ 并延长交 $ \odot O $ 于点 $ E $,连接 $ EC $. 若 $ AB = 8,CD = 2 $,则 $ EC $ 的长为

$2\sqrt{13}$
.
答案:$2\sqrt{13}$
解析:
设⊙O的半径为$r$,∵OD⊥AB于C,AB=8,∴AC=4,OC=OD-CD=r-2。在Rt△OAC中,由勾股定理得$r^2=4^2+(r-2)^2$,解得$r=5$,则OC=3,AE=10(直径)。连接BE,∵AE为直径,∴∠ABE=90°。在Rt△ABE中,BE=$\sqrt{AE^2-AB^2}=\sqrt{10^2-8^2}=6$。在Rt△BCE中,BC=4,BE=6,∴EC=$\sqrt{BC^2+BE^2}=\sqrt{4^2+6^2}=2\sqrt{13}$。
16. 如图, $ BC = 8\sqrt{3}cm $, $ D $ 是线段 $ BC $ 上的一动点,分别以 $ BD、CD $ 为边在 $ BC $ 的同侧作等边三角形 $ ABD $ 和等边三角形 $ CDE,AC、BE $ 相交于点 $ P $,则点 $ D $ 从点 $ B $ 运动到点 $ C $ 时,点 $ P $ 的运动路径长(含与点 $ B、C $ 重合)为

16π/3
.
答案:16π/3
解析:
连接BP、CP,易证△ADC≌△BDE(SAS),得∠DAC=∠EBD。在△BPC中,∠PBC+∠PCB=∠DAC+∠ACB=60°(△ADC中∠ADC=120°),故∠BPC=120°(定值)。点P轨迹是以BC为弦,圆周角120°的圆弧(BC上方)。设圆心为O,BC=8√3,弦长公式得半径R=8,圆心角∠BOC=120°。弧长=120°/360°×2π×8=16π/3。
17. 解下列一元二次方程(每题6分,共18分):
(1) $ x^{2}-3x + 2 = 0 $;
(2) $ (3x - 2)^{2}= (x + 4)^{2} $;
(3) $ 2x^{2}-3x - 1 = 0 $.
(1) $ x^{2}-3x + 2 = 0 $;
(2) $ (3x - 2)^{2}= (x + 4)^{2} $;
(3) $ 2x^{2}-3x - 1 = 0 $.
答案:(1)
因式分解法:
$x^{2}-3x + 2=(x - 1)(x - 2)=0$
则$x - 1 = 0$或$x - 2 = 0$
解得$x_{1}=1$,$x_{2}=2$
(2)
移项得$(3x - 2)^{2}-(x + 4)^{2}=0$
根据平方差公式$a^2-b^2=(a+b)(a-b)$,这里$a = 3x - 2$,$b = x + 4$
$(3x - 2+x + 4)(3x - 2-(x + 4))=0$
$(4x + 2)(2x - 6)=0$
$2(2x+1)×2(x - 3)=0$
$(2x + 1)(x - 3)=0$
则$2x+1 = 0$或$x - 3 = 0$
解得$x_{1}=-\frac{1}{2}$,$x_{2}=3$
(3)
对于一元二次方程$ax^{2}+bx+c = 0(a\neq0)$,这里$a = 2$,$b=-3$,$c = - 1$
根据求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$
先求$\Delta=b^{2}-4ac=(-3)^{2}-4×2×(-1)=9 + 8=17$
则$x=\frac{3\pm\sqrt{17}}{2×2}=\frac{3\pm\sqrt{17}}{4}$
所以$x_{1}=\frac{3+\sqrt{17}}{4}$,$x_{2}=\frac{3-\sqrt{17}}{4}$
因式分解法:
$x^{2}-3x + 2=(x - 1)(x - 2)=0$
则$x - 1 = 0$或$x - 2 = 0$
解得$x_{1}=1$,$x_{2}=2$
(2)
移项得$(3x - 2)^{2}-(x + 4)^{2}=0$
根据平方差公式$a^2-b^2=(a+b)(a-b)$,这里$a = 3x - 2$,$b = x + 4$
$(3x - 2+x + 4)(3x - 2-(x + 4))=0$
$(4x + 2)(2x - 6)=0$
$2(2x+1)×2(x - 3)=0$
$(2x + 1)(x - 3)=0$
则$2x+1 = 0$或$x - 3 = 0$
解得$x_{1}=-\frac{1}{2}$,$x_{2}=3$
(3)
对于一元二次方程$ax^{2}+bx+c = 0(a\neq0)$,这里$a = 2$,$b=-3$,$c = - 1$
根据求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$
先求$\Delta=b^{2}-4ac=(-3)^{2}-4×2×(-1)=9 + 8=17$
则$x=\frac{3\pm\sqrt{17}}{2×2}=\frac{3\pm\sqrt{17}}{4}$
所以$x_{1}=\frac{3+\sqrt{17}}{4}$,$x_{2}=\frac{3-\sqrt{17}}{4}$
18. (8分)如图,石拱桥的桥顶到水面的距离 $ CD $ 为 $ 8m $,桥拱半径 $ OC $ 为 $ 5m $,求水面宽 $ AB $.


答案:连接OA。
∵CD=8m,OC=5m,
∴OD=CD-OC=8-5=3m。
∵CD⊥AB,
∴AD=BD,∠ADO=90°。
在Rt△ADO中,OA=OC=5m,OD=3m,
由勾股定理得:AD²+OD²=OA²,
即AD²+3²=5²,
AD²=25-9=16,
AD=4m。
∴AB=2AD=2×4=8m。
答:水面宽AB为8m。
∵CD=8m,OC=5m,
∴OD=CD-OC=8-5=3m。
∵CD⊥AB,
∴AD=BD,∠ADO=90°。
在Rt△ADO中,OA=OC=5m,OD=3m,
由勾股定理得:AD²+OD²=OA²,
即AD²+3²=5²,
AD²=25-9=16,
AD=4m。
∴AB=2AD=2×4=8m。
答:水面宽AB为8m。