19. (8分)已知关于 $ x $ 的方程 $ 2x^{2}-kx + 1 = 0 $ 的一个解与方程 $ \frac{2x + 1}{1 - x}= 4 $ 的解相同.
(1) 求 $ k $ 的值;
(2) 求方程 $ 2x^{2}-kx + 1 = 0 $ 的另一个解.
(1) 求 $ k $ 的值;
(2) 求方程 $ 2x^{2}-kx + 1 = 0 $ 的另一个解.
答案:(1)$k = 3$;(2)另一个解为$1$。
解析:
(1)解方程$\frac{2x + 1}{1 - x}=4$:
两边同乘$1 - x$得$2x + 1 = 4(1 - x)$,
展开得$2x + 1 = 4 - 4x$,
移项合并得$6x = 3$,解得$x = \frac{1}{2}$。
检验:$x = \frac{1}{2}$时,$1 - x = \frac{1}{2} \neq 0$,故$x = \frac{1}{2}$是原分式方程的解。
将$x = \frac{1}{2}$代入$2x^2 - kx + 1 = 0$:
$2\left(\frac{1}{2}\right)^2 - k\left(\frac{1}{2}\right) + 1 = 0$,
即$2 × \frac{1}{4} - \frac{k}{2} + 1 = 0$,
化简得$\frac{1}{2} - \frac{k}{2} + 1 = 0$,
$\frac{3}{2} - \frac{k}{2} = 0$,解得$k = 3$。
(2)方程为$2x^2 - 3x + 1 = 0$,
因式分解得$(2x - 1)(x - 1) = 0$,
解得$x_1 = \frac{1}{2}$,$x_2 = 1$,
故另一个解为$1$。
两边同乘$1 - x$得$2x + 1 = 4(1 - x)$,
展开得$2x + 1 = 4 - 4x$,
移项合并得$6x = 3$,解得$x = \frac{1}{2}$。
检验:$x = \frac{1}{2}$时,$1 - x = \frac{1}{2} \neq 0$,故$x = \frac{1}{2}$是原分式方程的解。
将$x = \frac{1}{2}$代入$2x^2 - kx + 1 = 0$:
$2\left(\frac{1}{2}\right)^2 - k\left(\frac{1}{2}\right) + 1 = 0$,
即$2 × \frac{1}{4} - \frac{k}{2} + 1 = 0$,
化简得$\frac{1}{2} - \frac{k}{2} + 1 = 0$,
$\frac{3}{2} - \frac{k}{2} = 0$,解得$k = 3$。
(2)方程为$2x^2 - 3x + 1 = 0$,
因式分解得$(2x - 1)(x - 1) = 0$,
解得$x_1 = \frac{1}{2}$,$x_2 = 1$,
故另一个解为$1$。
20. (10分)如图,一窗户由矩形和弓形组成.已知弓形的跨度 $ AB = 3m $,弓形的高 $ EF = 1m $. 现计划安装玻璃,请你求出 $ \overset{\frown}{AB} $ 所在 $ \odot O $ 的半径.
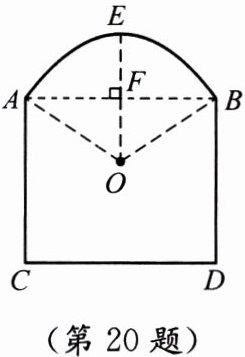

答案:设$\odot O$的半径为$R$m。
根据题意,$AB = 3$m,所以$AF=\frac{1}{2}AB = 1.5$m(垂径定理,垂直于弦的直径平分弦)。
在$Rt\triangle AOF$中,$OF = R - EF=(R - 1)$m,$OA = R$m。
根据勾股定理$OA^{2}=OF^{2}+AF^{2}$,可得:
$R^{2}=(R - 1)^{2}+1.5^{2}$
$R^{2}=R^{2}-2R + 1+2.25$
$2R=3.25$
$R = 1.625$
综上,$\overset{\frown}{AB}$所在$\odot O$的半径为$1.625$m。
根据题意,$AB = 3$m,所以$AF=\frac{1}{2}AB = 1.5$m(垂径定理,垂直于弦的直径平分弦)。
在$Rt\triangle AOF$中,$OF = R - EF=(R - 1)$m,$OA = R$m。
根据勾股定理$OA^{2}=OF^{2}+AF^{2}$,可得:
$R^{2}=(R - 1)^{2}+1.5^{2}$
$R^{2}=R^{2}-2R + 1+2.25$
$2R=3.25$
$R = 1.625$
综上,$\overset{\frown}{AB}$所在$\odot O$的半径为$1.625$m。
21. (10分)某商场服装柜台在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为了迎接儿童节,商场决定适度降价.经市场调查发现:如果每件童装降价1元,那么平均每天可多售出2件.
(1) 如果要平均每天盈利1200元,那么每件童装应降价多少元?
(2) 若要盈利最多,则每件童装应降价多少元?(用配方法)
(1) 如果要平均每天盈利1200元,那么每件童装应降价多少元?
(2) 若要盈利最多,则每件童装应降价多少元?(用配方法)
答案:(1)设每件童装应降价$x$元,根据题意,得$(40 - x)(20 + 2x) = 1200$。
展开并整理:$-2x^2 + 60x + 800 = 1200$,即$x^2 - 30x + 200 = 0$。
因式分解:$(x - 10)(x - 20) = 0$,解得$x_1 = 10$,$x_2 = 20$。
(2)设总盈利为$y$元,则$y = (40 - x)(20 + 2x) = -2x^2 + 60x + 800$。
配方:$y = -2(x^2 - 30x) + 800 = -2[(x - 15)^2 - 225] + 800 = -2(x - 15)^2 + 1250$。
∵$-2 < 0$,∴当$x = 15$时,$y$有最大值。
(1)每件童装应降价10元或20元;(2)每件童装应降价15元。
展开并整理:$-2x^2 + 60x + 800 = 1200$,即$x^2 - 30x + 200 = 0$。
因式分解:$(x - 10)(x - 20) = 0$,解得$x_1 = 10$,$x_2 = 20$。
(2)设总盈利为$y$元,则$y = (40 - x)(20 + 2x) = -2x^2 + 60x + 800$。
配方:$y = -2(x^2 - 30x) + 800 = -2[(x - 15)^2 - 225] + 800 = -2(x - 15)^2 + 1250$。
∵$-2 < 0$,∴当$x = 15$时,$y$有最大值。
(1)每件童装应降价10元或20元;(2)每件童装应降价15元。
22. (12分)如图,已知 $ \odot O $ 的半径为1, $ DE $ 是 $ \odot O $ 的直径,过点 $ D $ 作 $ \odot O $ 的切线 $ AD,C $ 是 $ AD $ 的中点, $ AE $ 交 $ \odot O $ 于点 $ B $,四边形 $ BCOE $ 是平行四边形.
(1) 求 $ AD $ 的长.
(2) $ BC $ 是 $ \odot O $ 的切线吗? 若是,给出证明;若不是,说明理由.

(1) 求 $ AD $ 的长.
(2) $ BC $ 是 $ \odot O $ 的切线吗? 若是,给出证明;若不是,说明理由.

答案:(1) $ 2 $;(2) 是,证明见上。
解析:
(1) 设 $ AD = x $,以 $ D $ 为原点,$ DE $ 所在直线为 $ x $ 轴,$ AD $ 所在直线为 $ y $ 轴建立坐标系。则 $ D(0,0) $,$ E(2,0) $,$ O(1,0) $,$ A(0,x) $,$ C(0,\frac{x}{2}) $。
直线 $ AE $ 方程:$ y = -\frac{x}{2}x + x $。
⊙$ O $ 方程:$ (x-1)^2 + y^2 = 1 $。
∵ 四边形 $ BCOE $ 是平行四边形,∴ $ \overrightarrow{CB} = \overrightarrow{OE} = (1,0) $,故 $ B(1,\frac{x}{2}) $。
将 $ B(1,\frac{x}{2}) $ 代入⊙$ O $ 方程:$ (1-1)^2 + (\frac{x}{2})^2 = 1 $,解得 $ x = 2 $。
∴ $ AD = 2 $。
(2) 是切线。证明如下:
由(1)得 $ B(1,1) $,$ O(1,0) $,$ C(0,1) $。
$ OB = \sqrt{(1-1)^2 + (1-0)^2} = 1 $,$ BC = \sqrt{(1-0)^2 + (1-1)^2} = 1 $,$ OC = \sqrt{(1-0)^2 + (0-1)^2} = \sqrt{2} $。
∵ $ OB^2 + BC^2 = 1 + 1 = 2 = OC^2 $,∴ $ \angle OBC = 90^\circ $,即 $ OB \perp BC $。
∵ $ OB $ 是半径,∴ $ BC $ 是⊙$ O $ 的切线。
直线 $ AE $ 方程:$ y = -\frac{x}{2}x + x $。
⊙$ O $ 方程:$ (x-1)^2 + y^2 = 1 $。
∵ 四边形 $ BCOE $ 是平行四边形,∴ $ \overrightarrow{CB} = \overrightarrow{OE} = (1,0) $,故 $ B(1,\frac{x}{2}) $。
将 $ B(1,\frac{x}{2}) $ 代入⊙$ O $ 方程:$ (1-1)^2 + (\frac{x}{2})^2 = 1 $,解得 $ x = 2 $。
∴ $ AD = 2 $。
(2) 是切线。证明如下:
由(1)得 $ B(1,1) $,$ O(1,0) $,$ C(0,1) $。
$ OB = \sqrt{(1-1)^2 + (1-0)^2} = 1 $,$ BC = \sqrt{(1-0)^2 + (1-1)^2} = 1 $,$ OC = \sqrt{(1-0)^2 + (0-1)^2} = \sqrt{2} $。
∵ $ OB^2 + BC^2 = 1 + 1 = 2 = OC^2 $,∴ $ \angle OBC = 90^\circ $,即 $ OB \perp BC $。
∵ $ OB $ 是半径,∴ $ BC $ 是⊙$ O $ 的切线。