1. 方程$x^{2}-16= 0$的根为(
A.$x = 4$
B.$x = -4$
C.$x_{1}= 4,x_{2}= -4$
D.$x_{1}= 2,x_{2}= -2$
C
)A.$x = 4$
B.$x = -4$
C.$x_{1}= 4,x_{2}= -4$
D.$x_{1}= 2,x_{2}= -2$
答案:C
解析:
由方程$x^{2}-16=0$,移项得$x^{2}=16$,开平方得$x=\pm4$,即$x_{1}=4,x_{2}=-4$。
2. 在用配方法解方程$x^{2}-4x + 3 = 0$的过程中,下列变形中,正确的是(
A.$x^{2}-4x+(-2)^{2}= 7$
B.$x^{2}-4x+(-2)^{2}= 1$
C.$(x + 2)^{2}= 1$
D.$(x - 1)^{2}= 2$
B
)A.$x^{2}-4x+(-2)^{2}= 7$
B.$x^{2}-4x+(-2)^{2}= 1$
C.$(x + 2)^{2}= 1$
D.$(x - 1)^{2}= 2$
答案:B
解析:
原方程为 $x^{2}-4x + 3 = 0$,移项得 $x^{2}-4x = -3$。
配方时,加上一次项系数一半的平方,即 $(-4 ÷ 2)^2 = 4$,得 $x^{2}-4x + 4 = 1$,即 $(x-2)^2 = 1$(该式未列出,继续分析选项)。
选项 A:$x^{2}-4x+(-2)^{2}= 7$,左边为 $x^{2}-4x+4$,但等式右边应为 $1$,错误。
选项 B:$x^{2}-4x+(-2)^{2}= 1$,与配方结果一致,正确。
选项 C:$(x + 2)^{2}= 1$,配方结果应为 $(x-2)^2 = 1$,错误。
选项 D:$(x - 1)^{2}= 2$,与配方结果不符,错误。
配方时,加上一次项系数一半的平方,即 $(-4 ÷ 2)^2 = 4$,得 $x^{2}-4x + 4 = 1$,即 $(x-2)^2 = 1$(该式未列出,继续分析选项)。
选项 A:$x^{2}-4x+(-2)^{2}= 7$,左边为 $x^{2}-4x+4$,但等式右边应为 $1$,错误。
选项 B:$x^{2}-4x+(-2)^{2}= 1$,与配方结果一致,正确。
选项 C:$(x + 2)^{2}= 1$,配方结果应为 $(x-2)^2 = 1$,错误。
选项 D:$(x - 1)^{2}= 2$,与配方结果不符,错误。
3. 若$4y^{2}-my + 25$是一个完全平方式,则$m$的值为(
A.10
B.$\pm10$
C.20
D.$\pm20$
D
)A.10
B.$\pm10$
C.20
D.$\pm20$
答案:D
解析:
要使$4y^{2}-my + 25$为完全平方式,可设其为$(2y \pm 5)^2$,展开得$4y^2 \pm 20y + 25$。对比系数,$-m = \pm 20$,故$m = \pm 20$。
4. 一元二次方程$x^{2}-2x + m = 0$总有实数根,则$m$应满足的条件是(
A.$m>1$
B.$m = 1$
C.$m<1$
D.$m\leq1$
D
)A.$m>1$
B.$m = 1$
C.$m<1$
D.$m\leq1$
答案:D
解析:
对于一元二次方程 $x^{2}-2x + m = 0$,其判别式为 $\Delta=b^{2}-4ac$,其中 $a = 1$,$b=-2$,$c = m$,则 $\Delta=(-2)^{2}-4×1× m=4 - 4m$。
因为方程总有实数根,所以 $\Delta\geqslant0$,即 $4-4m\geqslant0$,$4\geqslant4m$,解得 $m\leqslant1$。
因为方程总有实数根,所以 $\Delta\geqslant0$,即 $4-4m\geqslant0$,$4\geqslant4m$,解得 $m\leqslant1$。
5. 等腰三角形的底和腰是方程$x^{2}-6x + 8 = 0$的两个根,这个三角形的周长为(
A.8
B.10
C.8或10
D.无法确定
B
)A.8
B.10
C.8或10
D.无法确定
答案:B
解析:
解方程$x^{2}-6x + 8 = 0$,因式分解得$(x-2)(x-4)=0$,所以$x_1=2$,$x_2=4$。
若底为2,腰为4,满足三角形两边之和大于第三边($4+4>2$),周长为$2+4+4=10$;
若底为4,腰为2,不满足三角形条件($2+2=4$,不满足两边之和大于第三边)。
故只有第一种情况成立,周长为10。
若底为2,腰为4,满足三角形两边之和大于第三边($4+4>2$),周长为$2+4+4=10$;
若底为4,腰为2,不满足三角形条件($2+2=4$,不满足两边之和大于第三边)。
故只有第一种情况成立,周长为10。
6. 在半径为1的$\odot O$中,$120^{\circ}$的圆心角所对的弧长是(
A.$\frac{\pi}{3}$
B.$\frac{2\pi}{3}$
C.$\pi$
D.$\frac{3\pi}{2}$
B
)A.$\frac{\pi}{3}$
B.$\frac{2\pi}{3}$
C.$\pi$
D.$\frac{3\pi}{2}$
答案:B
解析:
已知圆的半径$r = 1$,圆心角$n = 120^{\circ}$,根据弧长公式$l=\frac{n\pi r}{180}$,可得弧长$l=\frac{120\pi×1}{180}=\frac{2\pi}{3}$。
7. 已知$AB为\odot O$的弦,$OC\perp AB$,垂足为$C$,若$OA = 10,AB = 16$,则$OC$的长为(
A.12
B.10
C.6
D.8
C
)A.12
B.10
C.6
D.8
答案:C
解析:
根据题意,$OC \perp AB$,所以$C$为$AB$的中点(垂径定理),即$AC = \frac{AB}{2} = \frac{16}{2} = 8$。
在直角三角形$OAC$中,已知$OA = 10$,$AC = 8$,根据勾股定理,有:
$OC = \sqrt{OA^{2} - AC^{2}} = \sqrt{10^{2} - 8^{2}} = \sqrt{100 - 64} = \sqrt{36} = 6$。
在直角三角形$OAC$中,已知$OA = 10$,$AC = 8$,根据勾股定理,有:
$OC = \sqrt{OA^{2} - AC^{2}} = \sqrt{10^{2} - 8^{2}} = \sqrt{100 - 64} = \sqrt{36} = 6$。
8. 某校要组织一次排球邀请赛,参赛的每支队之间都要比赛1场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛.设比赛组织者应邀请$x$支队参赛,则$x$满足的关系式为(
A.$\frac{1}{2}x(x + 1)= 28$
B.$\frac{1}{2}x(x - 1)= 28$
C.$x(x + 1)= 28$
D.$x(x - 1)= 28$
B
)A.$\frac{1}{2}x(x + 1)= 28$
B.$\frac{1}{2}x(x - 1)= 28$
C.$x(x + 1)= 28$
D.$x(x - 1)= 28$
答案:B
解析:
若有$x$支队伍参赛,则每支队伍需要和其他$(x - 1)$支队伍比赛1场。
由于两支队之间的比赛只计算1次,因此总的比赛场数为$\frac{1}{2}x(x - 1)$。
根据题意,总比赛场数为$7 × 4 = 28$场。
因此,$x$满足的关系式为$\frac{1}{2}x(x - 1) = 28$。
由于两支队之间的比赛只计算1次,因此总的比赛场数为$\frac{1}{2}x(x - 1)$。
根据题意,总比赛场数为$7 × 4 = 28$场。
因此,$x$满足的关系式为$\frac{1}{2}x(x - 1) = 28$。
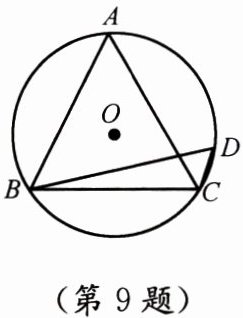
9. 如图,在$\odot O$中,$\angle ACB= \angle D = 60^{\circ},AC = 3,\triangle ABC$的周长为______
9
.
答案:9
解析:
由于$\angle ACB=\angle D=60^{\circ}$,根据同弧所对的圆周角相等,
可得$\angle A=\angle D=60^{\circ}$,
所以在$\triangle ABC$中,$\angle A = 60^{\circ}$,$\angle ACB = 60^{\circ}$,则$\angle ABC=60^{\circ}$,
所以$\triangle ABC$是等边三角形,
已知$AC = 3$,根据等边三角形三边相等,可得$AB = BC = AC = 3$,
那么$\triangle ABC$的周长为$3×3 = 9$。
可得$\angle A=\angle D=60^{\circ}$,
所以在$\triangle ABC$中,$\angle A = 60^{\circ}$,$\angle ACB = 60^{\circ}$,则$\angle ABC=60^{\circ}$,
所以$\triangle ABC$是等边三角形,
已知$AC = 3$,根据等边三角形三边相等,可得$AB = BC = AC = 3$,
那么$\triangle ABC$的周长为$3×3 = 9$。
10. 如图,点$D在以AC为直径的\odot O$上,如果$\angle BDC = 20^{\circ}$,那么$\angle ACB = $

70
$^{\circ}$.
答案:$70$
解析:
连接$AB$。
因为$AC$是$\odot O$的直径,根据直径所对的圆周角是直角,所以$\angle ABC = 90^{\circ}$。
已知$\angle BDC = 20^{\circ}$,根据同弧所对的圆周角相等,可得$\angle BAC=\angle BDC = 20^{\circ}$。
在$\triangle ABC$中,根据三角形内角和为$180^{\circ}$,则$\angle ACB=180^{\circ}-\angle ABC - \angle BAC=180^{\circ}-90^{\circ}-20^{\circ}=70^{\circ}$。
因为$AC$是$\odot O$的直径,根据直径所对的圆周角是直角,所以$\angle ABC = 90^{\circ}$。
已知$\angle BDC = 20^{\circ}$,根据同弧所对的圆周角相等,可得$\angle BAC=\angle BDC = 20^{\circ}$。
在$\triangle ABC$中,根据三角形内角和为$180^{\circ}$,则$\angle ACB=180^{\circ}-\angle ABC - \angle BAC=180^{\circ}-90^{\circ}-20^{\circ}=70^{\circ}$。