11. 已知四边形$ABCD内接于\odot O$,且$\angle A$、$\angle C的度数比为1:2$,则$\angle BOD = $
120
$^{\circ}$.答案:$120$
解析:
因为四边形$ABCD$内接于$\odot O$,根据圆内接四边形的性质,对角互补,即$\angle A + \angle C = 180^{\circ}$。
已知$\angle A$与$\angle C$的度数比为$1:2$,设$\angle A = x$,则$\angle C = 2x$,那么$x + 2x = 180^{\circ}$,
即$3x = 180^{\circ}$,解得$x = 60^{\circ}$,所以$\angle A = 60^{\circ}$。
在$\odot O$中,同弧所对的圆心角是圆周角的$2$倍,$\angle BOD$与$\angle A$分别是弧$BD$所对的圆心角和圆周角,所以$\angle BOD = 2\angle A = 120^{\circ}$。
已知$\angle A$与$\angle C$的度数比为$1:2$,设$\angle A = x$,则$\angle C = 2x$,那么$x + 2x = 180^{\circ}$,
即$3x = 180^{\circ}$,解得$x = 60^{\circ}$,所以$\angle A = 60^{\circ}$。
在$\odot O$中,同弧所对的圆心角是圆周角的$2$倍,$\angle BOD$与$\angle A$分别是弧$BD$所对的圆心角和圆周角,所以$\angle BOD = 2\angle A = 120^{\circ}$。
12. 已知圆锥底面半径是2,母线长是4,则圆锥的侧面展开图的扇形圆心角的度数为
180
$^{\circ}$.答案:180
解析:
设圆锥侧面展开图的扇形圆心角的度数为$n^{\circ}$。
圆锥底面周长为$2\pi×2 = 4\pi$,圆锥侧面展开图扇形的弧长公式为$\frac{n\pi×4}{180}$,由于圆锥底面周长等于侧面展开图扇形的弧长,则$\frac{n\pi×4}{180}=4\pi$,
两边同时除以$4\pi$可得:$\frac{n}{180}=1$,
解得$n = 180$。
圆锥底面周长为$2\pi×2 = 4\pi$,圆锥侧面展开图扇形的弧长公式为$\frac{n\pi×4}{180}$,由于圆锥底面周长等于侧面展开图扇形的弧长,则$\frac{n\pi×4}{180}=4\pi$,
两边同时除以$4\pi$可得:$\frac{n}{180}=1$,
解得$n = 180$。
13. 一副量角器与一块含$30^{\circ}$角的三角尺按如图所示放置,三角尺的顶点$C恰好落在量角器的直径MN$上,顶点$A$、$B$落在量角器的圆弧上,且$AB// MN$.若$AB = 8$,则量角器的直径$MN = $
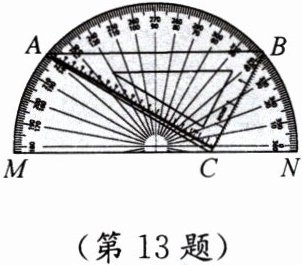
8√13
.
答案:8√13
解析:
设量角器的圆心为O,半径为R,连接OA、OB。因为AB//MN,过O作OD⊥AB于D,由垂径定理得AD=AB/2=4。设OD=d,在Rt△OAD中,AD²+OD²=OA²,即4²+d²=R²,d²=R²-16。
三角尺ABC为含30°角的直角三角形,∠C=30°,∠B=90°(AB//MN,BC⊥MN),则BC=d,AB=8。在Rt△ABC中,tan30°=AB/BC,即8/d=√3/3,解得d=8√3。
代入d²=R²-16,得(8√3)²=R²-16,192=R²-16,R²=208,R=4√13,故直径MN=2R=8√13。
三角尺ABC为含30°角的直角三角形,∠C=30°,∠B=90°(AB//MN,BC⊥MN),则BC=d,AB=8。在Rt△ABC中,tan30°=AB/BC,即8/d=√3/3,解得d=8√3。
代入d²=R²-16,得(8√3)²=R²-16,192=R²-16,R²=208,R=4√13,故直径MN=2R=8√13。
14. 写出一个以$-1和-2$为两根的一元二次方程(二次项系数为1):
$x^{2}+3x+2=0$
.答案:$x^{2}+3x+2=0$
解析:
设方程的两根为$x_1 = -1$和$x_2 = -2$,根据一元二次方程的性质,方程可以表示为$(x - x_1)(x - x_2) = 0$,即$(x - (-1))(x - (-2)) = 0$,化简得$(x + 1)(x + 2) = 0$,进一步展开得到$x^2 + 3x + 2 = 0$。
15. 已知关于$x的方程x^{2}+(1 - m)x+\frac{m^{2}}{4}= 0$有两个不相等的实数根,则$m$的最大整数值是
0
.答案:0
解析:
方程 $x^{2} + (1 - m)x + \frac{m^{2}}{4} = 0$ 有两个不相等的实数根,需满足判别式 $\Delta > 0$。
判别式为:
$\Delta = (1 - m)^{2} - 4 × 1 × \frac{m^{2}}{4}$
$= 1 - 2m + m^{2} - m^{2}$
$ = 1 - 2m$
要求 $\Delta > 0$,即:
$1 - 2m > 0$
解得:
$m < 0.5$
因此,$m$ 的最大整数值应小于 0.5,所以 $m$ 的最大整数值是 0。
判别式为:
$\Delta = (1 - m)^{2} - 4 × 1 × \frac{m^{2}}{4}$
$= 1 - 2m + m^{2} - m^{2}$
$ = 1 - 2m$
要求 $\Delta > 0$,即:
$1 - 2m > 0$
解得:
$m < 0.5$
因此,$m$ 的最大整数值应小于 0.5,所以 $m$ 的最大整数值是 0。
16. 如图,四边形$ABCD$为矩形,$AB = 3,BC = 4,P是线段BC$上一动点,$M为线段AP$上一点,$\angle ADM= \angle BAP$,则$BM$的最小值为______

2
.
答案:2
解析:
以A为原点,AB为x轴,AD为y轴建立平面直角坐标系。则A(0,0),B(3,0),D(0,4),设P(3,t)(0≤t≤4)。
AP所在直线方程为y=($\frac{t}{3}$)x。设M(m,$\frac{t}{3}$m)。
tan∠BAP=$\frac{t}{3}$,k$_{DM}$=$\frac{\frac{t}{3}m - 4}{m - 0}$=$\frac{tm - 12}{3m}$,∠ADM=∠BAP,tan∠ADM=$\frac{t}{3}$,则tan(π - ∠ADM)=-$\frac{t}{3}$,即$\frac{tm - 12}{3m}$=-$\frac{t}{3}$,解得m=$\frac{6}{t}$,故M($\frac{6}{t}$,2),M在直线y=2上。
BM=$\sqrt{(3 - \frac{6}{t})^2 + (0 - 2)^2}$,当$\frac{6}{t}$=3即t=2时,BM最小为2。
2
AP所在直线方程为y=($\frac{t}{3}$)x。设M(m,$\frac{t}{3}$m)。
tan∠BAP=$\frac{t}{3}$,k$_{DM}$=$\frac{\frac{t}{3}m - 4}{m - 0}$=$\frac{tm - 12}{3m}$,∠ADM=∠BAP,tan∠ADM=$\frac{t}{3}$,则tan(π - ∠ADM)=-$\frac{t}{3}$,即$\frac{tm - 12}{3m}$=-$\frac{t}{3}$,解得m=$\frac{6}{t}$,故M($\frac{6}{t}$,2),M在直线y=2上。
BM=$\sqrt{(3 - \frac{6}{t})^2 + (0 - 2)^2}$,当$\frac{6}{t}$=3即t=2时,BM最小为2。
2
17. 解下列方程(每题4分,共16分)
(1) $2x^{2}-4x - 7 = 0$(用配方法);
(2) $4x^{2}-3x - 1 = 0$(用公式法);
(3) $(x + 3)(x - 1)= 5$;
(4) $(3y - 2)^{2}= (2y - 3)^{2}$.
(1) $2x^{2}-4x - 7 = 0$(用配方法);
(2) $4x^{2}-3x - 1 = 0$(用公式法);
(3) $(x + 3)(x - 1)= 5$;
(4) $(3y - 2)^{2}= (2y - 3)^{2}$.
答案:(1) $2x^2 - 4x - 7 = 0$
两边同除以2:$x^2 - 2x - \frac{7}{2} = 0$
移项:$x^2 - 2x = \frac{7}{2}$
配方:$x^2 - 2x + 1 = \frac{7}{2} + 1$,即$(x - 1)^2 = \frac{9}{2}$
开方:$x - 1 = \pm \frac{3\sqrt{2}}{2}$
解得:$x_1 = 1 + \frac{3\sqrt{2}}{2}$,$x_2 = 1 - \frac{3\sqrt{2}}{2}$
(2) $4x^2 - 3x - 1 = 0$
$a = 4$,$b = -3$,$c = -1$
$\Delta = (-3)^2 - 4 × 4 × (-1) = 9 + 16 = 25$
$x = \frac{3 \pm \sqrt{25}}{2 × 4} = \frac{3 \pm 5}{8}$
解得:$x_1 = 1$,$x_2 = -\frac{1}{4}$
(3) $(x + 3)(x - 1) = 5$
展开:$x^2 + 2x - 3 = 5$
化简:$x^2 + 2x - 8 = 0$
因式分解:$(x + 4)(x - 2) = 0$
解得:$x_1 = -4$,$x_2 = 2$
(4) $(3y - 2)^2 = (2y - 3)^2$
移项:$(3y - 2)^2 - (2y - 3)^2 = 0$
因式分解:$[(3y - 2) - (2y - 3)][(3y - 2) + (2y - 3)] = 0$
化简:$(y + 1)(5y - 5) = 0$
解得:$y_1 = -1$,$y_2 = 1$
两边同除以2:$x^2 - 2x - \frac{7}{2} = 0$
移项:$x^2 - 2x = \frac{7}{2}$
配方:$x^2 - 2x + 1 = \frac{7}{2} + 1$,即$(x - 1)^2 = \frac{9}{2}$
开方:$x - 1 = \pm \frac{3\sqrt{2}}{2}$
解得:$x_1 = 1 + \frac{3\sqrt{2}}{2}$,$x_2 = 1 - \frac{3\sqrt{2}}{2}$
(2) $4x^2 - 3x - 1 = 0$
$a = 4$,$b = -3$,$c = -1$
$\Delta = (-3)^2 - 4 × 4 × (-1) = 9 + 16 = 25$
$x = \frac{3 \pm \sqrt{25}}{2 × 4} = \frac{3 \pm 5}{8}$
解得:$x_1 = 1$,$x_2 = -\frac{1}{4}$
(3) $(x + 3)(x - 1) = 5$
展开:$x^2 + 2x - 3 = 5$
化简:$x^2 + 2x - 8 = 0$
因式分解:$(x + 4)(x - 2) = 0$
解得:$x_1 = -4$,$x_2 = 2$
(4) $(3y - 2)^2 = (2y - 3)^2$
移项:$(3y - 2)^2 - (2y - 3)^2 = 0$
因式分解:$[(3y - 2) - (2y - 3)][(3y - 2) + (2y - 3)] = 0$
化简:$(y + 1)(5y - 5) = 0$
解得:$y_1 = -1$,$y_2 = 1$
解析:
(1)
解:$2x^{2}-4x=7$
$x^{2}-2x=\frac{7}{2}$
$x^{2}-2x + 1=\frac{7}{2}+ 1$
$(x - 1)^{2}=\frac{9}{2}$
$x - 1=\pm\frac{3\sqrt{2}}{2}$
$x_{1}=1+\frac{3\sqrt{2}}{2}$,$x_{2}=1-\frac{3\sqrt{2}}{2}$
(2)
解:$a = 4$,$b=-3$,$c=-1$
$\Delta=(-3)^{2}-4×4×(-1)=9 + 16=25$
$x=\frac{3\pm\sqrt{25}}{2×4}=\frac{3\pm5}{8}$
$x_{1}=1$,$x_{2}=-\frac{1}{4}$
(3)
解:$x^{2}+2x - 3=5$
$x^{2}+2x - 8=0$
$(x + 4)(x - 2)=0$
$x_{1}=-4$,$x_{2}=2$
(4)
解:$(3y - 2)^{2}-(2y - 3)^{2}=0$
$(3y - 2 + 2y - 3)(3y - 2 - 2y + 3)=0$
$(5y - 5)(y + 1)=0$
$y_{1}=1$,$y_{2}=-1$
18. (10分)在网格中画出符合下列条件的图形(保留画图痕迹,不写画图步骤).
(1) 画出所给图形关于直线$BE$对称的图形,并标出点$A$、$D的对应点A_{1}$、$D_{1}$;
(2) 画出一个与直线$CA$、$CA_{1}$都相切,且切点分别为点$A$、$A_{1}$的圆,并标出圆心$O$.

(1) 画出所给图形关于直线$BE$对称的图形,并标出点$A$、$D的对应点A_{1}$、$D_{1}$;
(2) 画出一个与直线$CA$、$CA_{1}$都相切,且切点分别为点$A$、$A_{1}$的圆,并标出圆心$O$.

答案:(1)图略(作出关于直线BE对称的图形,标出A₁、D₁,保留对称作图痕迹)。
(2)图略(作出过A且垂直于CA的直线,过A₁且垂直于CA₁的直线,两直线交点为圆心O,以OA为半径作圆,保留作图痕迹)。
(注:实际作答需在答题卡网格中完成作图,此处文字说明仅示意,具体以规范作图为准。)
(2)图略(作出过A且垂直于CA的直线,过A₁且垂直于CA₁的直线,两直线交点为圆心O,以OA为半径作圆,保留作图痕迹)。
(注:实际作答需在答题卡网格中完成作图,此处文字说明仅示意,具体以规范作图为准。)
19. (10分)已知$m是方程x^{2}-x - 2 = 0$的一个实数根,求代数式$(m^{2}-m)(m-\frac{2}{m}+1)$的值.
答案:4
解析:
因为m是方程$x^{2}-x - 2 = 0$的实数根,所以$m^{2}-m-2=0$。
由$m^{2}-m-2=0$,得$m^{2}-m=2$。
又因为$m\neq0$(若$m=0$,代入方程左边得$-2\neq0$),方程两边同除以$m$,得$m - 1-\frac{2}{m}=0$,即$m-\frac{2}{m}=1$。
则代数式$(m^{2}-m)(m-\frac{2}{m}+1)=2×(1 + 1)=2×2=4$。
由$m^{2}-m-2=0$,得$m^{2}-m=2$。
又因为$m\neq0$(若$m=0$,代入方程左边得$-2\neq0$),方程两边同除以$m$,得$m - 1-\frac{2}{m}=0$,即$m-\frac{2}{m}=1$。
则代数式$(m^{2}-m)(m-\frac{2}{m}+1)=2×(1 + 1)=2×2=4$。