1. 方程$x^{2}-5x= 0$的解是
(
A.$x _ { 1 } = 0$,$x _ { 2 } = - 5$
B.$x = 5$
C.$x _ { 1 } = 0$,$x _ { 2 } = 5$
D.$x = 0$
(
C
)A.$x _ { 1 } = 0$,$x _ { 2 } = - 5$
B.$x = 5$
C.$x _ { 1 } = 0$,$x _ { 2 } = 5$
D.$x = 0$
答案:C
解析:
原方程为 $x^{2} - 5x = 0$,提取公因式 $x$ 得 $x(x - 5) = 0$。
根据零因子定理,$x = 0$ 或 $x - 5 = 0$,解得 $x_1 = 0$,$x_2 = 5$。
根据零因子定理,$x = 0$ 或 $x - 5 = 0$,解得 $x_1 = 0$,$x_2 = 5$。
2. 设$x _ { 1 }$,$x _ { 2 }是方程x ^ { 2 } + 3 x - 3 = 0$的两个实数根,则$x _ { 1 } + x _ { 2 }$的值为
(
A.3
B.-3
C.1
D.-1
(
B
)A.3
B.-3
C.1
D.-1
答案:B
解析:
对于二次方程 $ax^{2} + bx + c = 0$,其两个根 $x_1$ 和 $x_2$ 的和由公式 $x_1 + x_2 = -\frac{b}{a}$ 给出。
对于给定的方程 $x^{2} + 3x - 3 = 0$,其中 $a = 1, b = 3$。
根据公式,有$x_1 + x_2 = -\frac{3}{1} = -3$。
对于给定的方程 $x^{2} + 3x - 3 = 0$,其中 $a = 1, b = 3$。
根据公式,有$x_1 + x_2 = -\frac{3}{1} = -3$。
3. 关于$x的一元二次方程x ^ { 2 } - 2 a x - 1 = 0$(其中$a$为常数)的根的情况是
(
A.有两个不相等的实数根
B.可能有实数根,也可能没有
C.有两个相等的实数根
D.没有实数根
(
A
)A.有两个不相等的实数根
B.可能有实数根,也可能没有
C.有两个相等的实数根
D.没有实数根
答案:A
解析:
对于一元二次方程 $x^{2}-2ax-1=0$,其判别式为:
$\Delta =(-2a)^{2} -4 × 1 × (-1) = 4a^{2} + 4$,
因为 $a^{2} \geq 0$,所以 $4a^{2} + 4 \gt 0$,
由于判别式 $\Delta \gt 0$,所以方程有两个不相等的实数根。
$\Delta =(-2a)^{2} -4 × 1 × (-1) = 4a^{2} + 4$,
因为 $a^{2} \geq 0$,所以 $4a^{2} + 4 \gt 0$,
由于判别式 $\Delta \gt 0$,所以方程有两个不相等的实数根。
4. 已知圆锥的底面半径为2,母线长为4,则它的侧面积为
(
A.$4 \pi$
B.$1 6 \pi$
C.$4 \sqrt { 3 } \pi$
D.$8 \pi$
(
D
)A.$4 \pi$
B.$1 6 \pi$
C.$4 \sqrt { 3 } \pi$
D.$8 \pi$
答案:D
解析:
圆锥的侧面积公式为$S = \pi r l$,其中$r$为底面半径,$l$为母线长。
已知$r = 2$,$l = 4$,代入公式得:
$S = \pi × 2 × 4 = 8\pi$。
已知$r = 2$,$l = 4$,代入公式得:
$S = \pi × 2 × 4 = 8\pi$。
5. 已知$\odot O$的半径是5,直线$l是\odot O$的切线,$P是l$上的任意一点,那么
(
A.$0 < O P < 5$
B.$O P = 5$
C.$O P > 5$
D.$O P \geqslant 5$
(
D
)A.$0 < O P < 5$
B.$O P = 5$
C.$O P > 5$
D.$O P \geqslant 5$
答案:D
解析:
因为直线$l$是$\odot O$的切线,设切点为$A$,则$OA \perp l$,且$OA = 5$。$P$是$l$上任意一点,当$P$与$A$重合时,$OP = OA = 5$;当$P$与$A$不重合时,$OP$为直角三角形$OAP$的斜边,所以$OP > OA = 5$。综上,$OP \geqslant 5$。
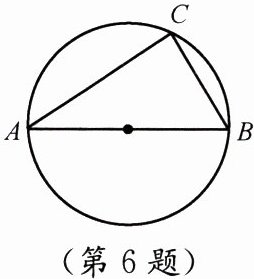
6. 如图,已知$AB是\triangle ABC$外接圆的直径,$\angle A = 3 5 ^ { \circ }$,则$\angle B$的度数是
(
A.$3 5 ^ { \circ }$
B.$4 5 ^ { \circ }$
C.$5 5 ^ { \circ }$
D.$6 5 ^ { \circ }$
(
C
)
A.$3 5 ^ { \circ }$
B.$4 5 ^ { \circ }$
C.$5 5 ^ { \circ }$
D.$6 5 ^ { \circ }$
答案:C
解析:
$\because AB$是$\triangle ABC$外接圆的直径,
$\therefore \angle C=90^{\circ}$(直径所对的圆周角是直角)。
在$\triangle ABC$中,
$\angle A = 35^{\circ}$,$\angle C = 90^{\circ}$,
根据三角形内角和为$180^{\circ}$,
可得$\angle B=180^{\circ}-\angle A - \angle C=180^{\circ}-35^{\circ}-90^{\circ}=55^{\circ}$。
$\therefore \angle C=90^{\circ}$(直径所对的圆周角是直角)。
在$\triangle ABC$中,
$\angle A = 35^{\circ}$,$\angle C = 90^{\circ}$,
根据三角形内角和为$180^{\circ}$,
可得$\angle B=180^{\circ}-\angle A - \angle C=180^{\circ}-35^{\circ}-90^{\circ}=55^{\circ}$。
7. 下列说法中,正确的是
(
A.“明天降雨的概率是50%”表示明天有半天都在降雨
B.数据4,4,5,5,0的中位数和众数都是5
C.要了解某批零件的合格率是否满足要求,应采用普查的方式
D.若甲、乙两组数中各有20个数据,平均数$\overline { x } _ { 甲 } = \overline { x } _ { 乙 }$,方差$s _ { 甲 } ^ { 2 } = 1 . 2 5$,$s _ { 乙 } ^ { 2 } = 0 . 9 6$,则说明乙组数据比甲组数据稳定
(
D
)A.“明天降雨的概率是50%”表示明天有半天都在降雨
B.数据4,4,5,5,0的中位数和众数都是5
C.要了解某批零件的合格率是否满足要求,应采用普查的方式
D.若甲、乙两组数中各有20个数据,平均数$\overline { x } _ { 甲 } = \overline { x } _ { 乙 }$,方差$s _ { 甲 } ^ { 2 } = 1 . 2 5$,$s _ { 乙 } ^ { 2 } = 0 . 9 6$,则说明乙组数据比甲组数据稳定
答案:D
解析:
本题可根据概率的意义、中位数和众数的定义、普查与抽查的适用情况以及方差的意义,对选项逐一进行分析。
选项A:
概率是反映事件发生机会的大小的概念,“明天降雨的概率是$50\%$”表示明天降雨的可能性是$50\%$,而不是明天有半天都在降雨,所以该选项错误。
选项B:
将数据$4$,$4$,$5$,$5$,$0$按照从小到大的顺序排列为$0$,$4$,$4$,$5$,$5$。
中位数是按顺序排列的一组数据中居于中间位置的数,如果数据有奇数个,则正中间的数字为中位数;如果数据有偶数个,则中间两位数的平均数为中位数。这组数据有$5$个,中间是第$3$个数$4$,所以中位数是$4$。
众数是一组数据中出现次数最多的数据,$4$和$5$都出现了$2$次,出现的次数最多,则众数是$4$和$5$。所以该选项错误。
选项C:
要了解某批零件的合格率是否满足要求,由于检测零件合格率具有破坏性,全面检测会使所有零件都被破坏,所以应采用抽查的方式,而不是普查的方式,所以该选项错误。
选项D:
方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定。
已知$s_{甲}^{2}=1.25$,$s_{乙}^{2}=0.96$,因为$s_{甲}^{2}>s_{乙}^{2}$,所以乙组数据比甲组数据稳定,该选项正确。
综上,答案是D。
选项A:
概率是反映事件发生机会的大小的概念,“明天降雨的概率是$50\%$”表示明天降雨的可能性是$50\%$,而不是明天有半天都在降雨,所以该选项错误。
选项B:
将数据$4$,$4$,$5$,$5$,$0$按照从小到大的顺序排列为$0$,$4$,$4$,$5$,$5$。
中位数是按顺序排列的一组数据中居于中间位置的数,如果数据有奇数个,则正中间的数字为中位数;如果数据有偶数个,则中间两位数的平均数为中位数。这组数据有$5$个,中间是第$3$个数$4$,所以中位数是$4$。
众数是一组数据中出现次数最多的数据,$4$和$5$都出现了$2$次,出现的次数最多,则众数是$4$和$5$。所以该选项错误。
选项C:
要了解某批零件的合格率是否满足要求,由于检测零件合格率具有破坏性,全面检测会使所有零件都被破坏,所以应采用抽查的方式,而不是普查的方式,所以该选项错误。
选项D:
方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定。
已知$s_{甲}^{2}=1.25$,$s_{乙}^{2}=0.96$,因为$s_{甲}^{2}>s_{乙}^{2}$,所以乙组数据比甲组数据稳定,该选项正确。
综上,答案是D。
8. 一只不透明的袋子中装有红、白、黄和黑4个除颜色外都相同的小球,从中任意摸出1个小球是白色小球的概率是
(
A.$\frac { 1 } { 2 }$
B.$\frac { 1 } { 3 }$
C.$\frac { 1 } { 4 }$
D.$\frac { 1 } { 6 }$
(
C
)A.$\frac { 1 } { 2 }$
B.$\frac { 1 } { 3 }$
C.$\frac { 1 } { 4 }$
D.$\frac { 1 } { 6 }$
答案:C
解析:
袋子中共有4个除颜色外都相同的小球,白色小球有1个,从中任意摸出1个小球是白色小球的概率是$\frac{1}{4}$。
9. 将一元二次方程$3x(x - 1) = 5$化成一般形式为
$3x^{2}-3x-5=0$
.答案:$3x^{2}-3x-5=0$
解析:
首先,将方程$3x(x - 1) = 5$展开,得到$3x^2 - 3x = 5$。
接着,将方程转化为一般形式,即$3x^2 - 3x - 5 = 0$。
接着,将方程转化为一般形式,即$3x^2 - 3x - 5 = 0$。
10. 某药品原价是每盒16元,连续两次降价后,现在售价是每盒9元,则该药品平均每次降价的百分率是
25%
.答案:$25\%$(按照题目要求若为填空题直接填$25\%$)
解析:
设平均每次降价的百分率为$x$,根据题意得$16(1 - x)^{2} = 9$,即$(1 - x)^{2}=\frac{9}{16}$,则$1 - x=\pm\frac{3}{4}$,当$1 - x=\frac{3}{4}$时,$x = 0.25 = 25\%$;当$1 - x=-\frac{3}{4}$时,$x = 1.75$(不合题意,舍去)。所以平均每次降价的百分率是$25\%$。