1. 某花圃用花盆培育花苗,每盆植入 3 株花苗时,平均单株盈利 3 元;每增加 1 株花苗,平均单株盈利就减少 0.5 元. 要使每盆的盈利达到 10 元,每盆应该植入多少株花苗?
答案:设每盆增加$x$株花苗,则每盆植入$(3 + x)$株,单株盈利为$(3 - 0.5x)$元。
依题意列方程:$(3 + x)(3 - 0.5x) = 10$
展开并整理:
$9 + 1.5x - 0.5x^2 = 10$
$-0.5x^2 + 1.5x - 1 = 0$
两边乘$-2$:$x^2 - 3x + 2 = 0$
因式分解:$(x - 1)(x - 2) = 0$
解得$x_1 = 1$,$x_2 = 2$
当$x = 1$时,株数为$3 + 1 = 4$;
当$x = 2$时,株数为$3 + 2 = 5$。
答:每盆应植入4株或5株花苗。
依题意列方程:$(3 + x)(3 - 0.5x) = 10$
展开并整理:
$9 + 1.5x - 0.5x^2 = 10$
$-0.5x^2 + 1.5x - 1 = 0$
两边乘$-2$:$x^2 - 3x + 2 = 0$
因式分解:$(x - 1)(x - 2) = 0$
解得$x_1 = 1$,$x_2 = 2$
当$x = 1$时,株数为$3 + 1 = 4$;
当$x = 2$时,株数为$3 + 2 = 5$。
答:每盆应植入4株或5株花苗。
2. 商场销售某种冰箱,每台进货价为 2500 元. 市场调研表明,当销售价为 2900 元时,平均每天能售出 8 台;当销售价每降低 50 元时,平均每天就能多售出 4 台. 商场要想使这种冰箱的销售利润平均每天达到 5000 元,每台冰箱的定价应为多少元?
答案:设每台冰箱应降价$x$个50元,则销售价为$(2900 - 50x)$元,每天能多售出$4x$台,实际售出量为$(8 + 4x)$台。
每台冰箱的利润为:
$(2900 - 50x) - 2500 = 400 - 50x$(元),
所以总利润为:
$(400 - 50x)(8 + 4x)$(元),
根据题意,总利润为5000元,所以我们可以建立方程:
$(400 - 50x)(8 + 4x) = 5000$,
展开并整理得:
$3200 + 1600x - 400x - 200x^{2} = 5000$,
进一步整理为:
$200x^{2} - 1200x + 1800 = 0$,
除以200得:
$x^{2} - 6x + 9 = 0$,
解得:
$x_{1} = x_{2} = 3$,
所以销售价为:
$2900 - 50 × 3 = 2750 × (或 2900 - 3 × 50=2750)$(元)(两个解相同,只计算一次),
另一种情况考虑方程:
$(400 - 50x)(8 + 4x) = 5000$,
也可以将5000表示为:
$20 × 250$,
并考虑每台利润与台数的乘积,但经过整理,方程仍然相同,所以解也唯一。
答:每台冰箱的定价应为2750元。
每台冰箱的利润为:
$(2900 - 50x) - 2500 = 400 - 50x$(元),
所以总利润为:
$(400 - 50x)(8 + 4x)$(元),
根据题意,总利润为5000元,所以我们可以建立方程:
$(400 - 50x)(8 + 4x) = 5000$,
展开并整理得:
$3200 + 1600x - 400x - 200x^{2} = 5000$,
进一步整理为:
$200x^{2} - 1200x + 1800 = 0$,
除以200得:
$x^{2} - 6x + 9 = 0$,
解得:
$x_{1} = x_{2} = 3$,
所以销售价为:
$2900 - 50 × 3 = 2750 × (或 2900 - 3 × 50=2750)$(元)(两个解相同,只计算一次),
另一种情况考虑方程:
$(400 - 50x)(8 + 4x) = 5000$,
也可以将5000表示为:
$20 × 250$,
并考虑每台利润与台数的乘积,但经过整理,方程仍然相同,所以解也唯一。
答:每台冰箱的定价应为2750元。
1. 某旅行社为吸引市民组团去森林风景区旅游,推出了如下优惠活动:如果人数不超过 25 人,人均旅游费用为 1000 元;如果人数超过 25 人,每增加 1 人,人均旅游费用降低 20 元,但人均旅游费用不得低于 700 元. 某单位组织员工去森林风景区旅游,共支付给该旅行社旅游费用 27000 元,该单位这次共有多少员工去森林风景区旅游?
答案:设该单位这次共有$x$名员工去森林风景区旅游。
因为$25×1000 = 25000\lt27000$,所以$x\gt25$。
人均旅游费用为$1000 - 20(x - 25)$元,总费用为$x[1000 - 20(x - 25)]$元,依题意列方程:
$x[1000 - 20(x - 25)] = 27000$
化简得:$x(1500 - 20x) = 27000$
即:$-20x^2 + 1500x - 27000 = 0$
两边同除以$-20$:$x^2 - 75x + 1350 = 0$
因式分解:$(x - 30)(x - 45) = 0$
解得:$x_1 = 30$,$x_2 = 45$
检验:
当$x = 45$时,人均费用$1000 - 20(45 - 25) = 600\lt700$,不合题意,舍去;
当$x = 30$时,人均费用$1000 - 20(30 - 25) = 900\geq700$,符合题意。
答:该单位这次共有30名员工去森林风景区旅游。
因为$25×1000 = 25000\lt27000$,所以$x\gt25$。
人均旅游费用为$1000 - 20(x - 25)$元,总费用为$x[1000 - 20(x - 25)]$元,依题意列方程:
$x[1000 - 20(x - 25)] = 27000$
化简得:$x(1500 - 20x) = 27000$
即:$-20x^2 + 1500x - 27000 = 0$
两边同除以$-20$:$x^2 - 75x + 1350 = 0$
因式分解:$(x - 30)(x - 45) = 0$
解得:$x_1 = 30$,$x_2 = 45$
检验:
当$x = 45$时,人均费用$1000 - 20(45 - 25) = 600\lt700$,不合题意,舍去;
当$x = 30$时,人均费用$1000 - 20(30 - 25) = 900\geq700$,符合题意。
答:该单位这次共有30名员工去森林风景区旅游。
2. 某商店新进一批 T 恤衫,每件进价 35 元,售价 55 元. 为增加销量,商店决定降价销售. 已知这种 T 恤衫的销售量 $ y $ (件) 与每件降价 $ x $ (元) ($ 0 \leqslant x < 20 $) 之间满足一次函数关系,其图像如图所示.
(1) 求 $ y $ 与 $ x $ 之间的函数表达式;
(2) 若在本次降价促销活动中,该商店获利 1760 元,则这种 T 恤衫每件的实际售价是多少元?
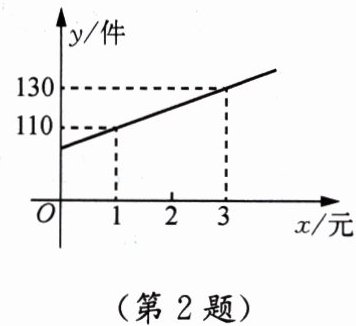
(1) 求 $ y $ 与 $ x $ 之间的函数表达式;
(2) 若在本次降价促销活动中,该商店获利 1760 元,则这种 T 恤衫每件的实际售价是多少元?

答案:(1) 设 $ y $ 与 $ x $ 之间的函数表达式为 $ y = kx + b $。由图像可知,当 $ x = 1 $ 时,$ y = 110 $;当 $ x = 3 $ 时,$ y = 130 $。将两点代入得:
$\begin{cases}110 = k + b \\130 = 3k + b\end{cases}$
解得 $ k = 10 $,$ b = 100 $。故函数表达式为 $ y = 10x + 100 $。
(2) 每件利润为 $ (55 - x - 35) = (20 - x) $ 元,销售量为 $ y = 10x + 100 $ 件。由总利润为 1760 元,得:
$(20 - x)(10x + 100) = 1760$
整理得 $ x^2 - 10x - 24 = 0 $,解得 $ x_1 = 12 $,$ x_2 = -2 $(舍去)。
实际售价为 $ 55 - 12 = 43 $ 元。
(1) $ y = 10x + 100 $;(2) 43 元。
$\begin{cases}110 = k + b \\130 = 3k + b\end{cases}$
解得 $ k = 10 $,$ b = 100 $。故函数表达式为 $ y = 10x + 100 $。
(2) 每件利润为 $ (55 - x - 35) = (20 - x) $ 元,销售量为 $ y = 10x + 100 $ 件。由总利润为 1760 元,得:
$(20 - x)(10x + 100) = 1760$
整理得 $ x^2 - 10x - 24 = 0 $,解得 $ x_1 = 12 $,$ x_2 = -2 $(舍去)。
实际售价为 $ 55 - 12 = 43 $ 元。
(1) $ y = 10x + 100 $;(2) 43 元。