3. 受益于新能源汽车产业的快速发展,某汽车零部件生产企业的利润逐年提高. 据统计,2022 年利润为 2 亿元,2024 年利润为 2.88 亿元.
(1) 求该企业从 2022 年到 2024 年利润的年平均增长率;
(2) 若利润的年平均增长率不变,该企业 2025 年的利润能否超过 3.5 亿元?
(1) 求该企业从 2022 年到 2024 年利润的年平均增长率;
(2) 若利润的年平均增长率不变,该企业 2025 年的利润能否超过 3.5 亿元?
答案:(1) 设该企业从 2022 年到 2024 年利润的年平均增长率为 $x$。
根据题意,2022 年利润为 2 亿元,2024 年利润为 2.88 亿元,列出方程:
$2(1 + x)^{2} = 2.88$,
解方程,得到:
$(1 + x)^{2} = 1.44$,
$1+x=\pm1.2$
由于增长率不能为负,舍去$x_2 = -2.2$,
得到$x = 0.2 = 20\%$。
答:该企业从 2022 年到 2024 年利润的年平均增长率为 $20\%$。
(2) 根据第一问的年平均增长率 $x = 20\%$,计算 2025 年的利润:
$2025年利润 = 2024年利润 × (1 + 增长率)$
$ = 2.88 × (1 + 20\%) $
$= 2.88 × 1.2 $
$= 3.456 (亿元)$
比较得 $3.456 \lt 3.5$。
答:该企业 2025 年的利润不能超过 3.5 亿元。
根据题意,2022 年利润为 2 亿元,2024 年利润为 2.88 亿元,列出方程:
$2(1 + x)^{2} = 2.88$,
解方程,得到:
$(1 + x)^{2} = 1.44$,
$1+x=\pm1.2$
由于增长率不能为负,舍去$x_2 = -2.2$,
得到$x = 0.2 = 20\%$。
答:该企业从 2022 年到 2024 年利润的年平均增长率为 $20\%$。
(2) 根据第一问的年平均增长率 $x = 20\%$,计算 2025 年的利润:
$2025年利润 = 2024年利润 × (1 + 增长率)$
$ = 2.88 × (1 + 20\%) $
$= 2.88 × 1.2 $
$= 3.456 (亿元)$
比较得 $3.456 \lt 3.5$。
答:该企业 2025 年的利润不能超过 3.5 亿元。
4. 某玩具厂生产一种玩具,据市场调查,每个玩具按 480 元销售,每天可销售 160 个;若销售单价每降低 1 元,每天可多售出 2 个. 已知每个玩具的固定成本为 360 元. 这种玩具的销售单价为多少元时,厂家每天可获利润 20000 元?
答案:设这种玩具的销售单价为$x$元。
每个玩具的利润为$(x - 360)$元。
原销售量为$160$个,单价每降低$1$元,销售量增加$2$个,因此销售量为$[160 + 2(480 - x)]$个。
根据题意,总利润为$20000$元,因此可列方程:
$(x - 360)[160 + 2(480 - x)] = 20000$
展开方程得:
$(x - 360)(160 + 960 - 2x) = 20000$
$(x - 360)(1120 - 2x) = 20000$
$1120x - 2x^2 - 360 × 1120 + 720x = 20000$
$-2x^2 + 1840x - 403200 = 20000$
$-2x^2 + 1840x - 423200 = 0$
$x^2 - 920x + 211600 = 0$
解得:
$x_{1} = x_{2} = 460$
答:这种玩具的销售单价为$460$元时,厂家每天可获利润$20000$元。
每个玩具的利润为$(x - 360)$元。
原销售量为$160$个,单价每降低$1$元,销售量增加$2$个,因此销售量为$[160 + 2(480 - x)]$个。
根据题意,总利润为$20000$元,因此可列方程:
$(x - 360)[160 + 2(480 - x)] = 20000$
展开方程得:
$(x - 360)(160 + 960 - 2x) = 20000$
$(x - 360)(1120 - 2x) = 20000$
$1120x - 2x^2 - 360 × 1120 + 720x = 20000$
$-2x^2 + 1840x - 403200 = 20000$
$-2x^2 + 1840x - 423200 = 0$
$x^2 - 920x + 211600 = 0$
解得:
$x_{1} = x_{2} = 460$
答:这种玩具的销售单价为$460$元时,厂家每天可获利润$20000$元。
1. 某农场要建一个矩形的养鸡场,养鸡场的一面靠墙(墙长为 25 m),另三面用木栅栏围成,木栅栏的总长度为 40 m.
(1) 养鸡场的面积能达到$ 180 m^2$吗?能达到$ 200 m^2$吗?
(2) 养鸡场的面积能达到$ 250 m^2$吗?如果能,请你给出设计方案;如果不能,请说明理由.
(1) 养鸡场的面积能达到$ 180 m^2$吗?能达到$ 200 m^2$吗?
(2) 养鸡场的面积能达到$ 250 m^2$吗?如果能,请你给出设计方案;如果不能,请说明理由.
答案:(1) 设与墙垂直的边长为$x\ m$,则与墙平行的边长为$(40 - 2x)\ m$,面积$S = x(40 - 2x)$。由题意得$40 - 2x > 0$且$40 - 2x \leq 25$,解得$7.5 \leq x < 20$。
当$S = 180$时,$x(40 - 2x) = 180$,即$x^2 - 20x + 90 = 0$,$\Delta = 400 - 360 = 40 > 0$,$x = 10 \pm \sqrt{10}$。$x = 10 + \sqrt{10} \approx 13.16$在$7.5 \leq x < 20$内,能达到$180\ m^2$。
当$S = 200$时,$x(40 - 2x) = 200$,即$(x - 10)^2 = 0$,$x = 10$。此时$40 - 2x = 20 \leq 25$,能达到$200\ m^2$。
(2) 当$S = 250$时,$x(40 - 2x) = 250$,即$x^2 - 20x + 125 = 0$,$\Delta = 400 - 500 = -100 < 0$,方程无实根,不能达到$250\ m^2$。
当$S = 180$时,$x(40 - 2x) = 180$,即$x^2 - 20x + 90 = 0$,$\Delta = 400 - 360 = 40 > 0$,$x = 10 \pm \sqrt{10}$。$x = 10 + \sqrt{10} \approx 13.16$在$7.5 \leq x < 20$内,能达到$180\ m^2$。
当$S = 200$时,$x(40 - 2x) = 200$,即$(x - 10)^2 = 0$,$x = 10$。此时$40 - 2x = 20 \leq 25$,能达到$200\ m^2$。
(2) 当$S = 250$时,$x(40 - 2x) = 250$,即$x^2 - 20x + 125 = 0$,$\Delta = 400 - 500 = -100 < 0$,方程无实根,不能达到$250\ m^2$。
2. 如图,在 $Rt\triangle ABC$ 中,$\angle B = 90^{\circ}$,$AB = BC = 12$ cm,$D$、$E$、$F$ 是动点,点 $D$ 从点 $A$ 出发,以 2 cm/s 的速度沿 $AB$ 向点 $B$ 移动,移动过程中始终保持 $DE// BC$,$DF// AC$. 点 $D$ 出发几秒时,四边形 $DFCE$ 的面积为 20 cm^2?
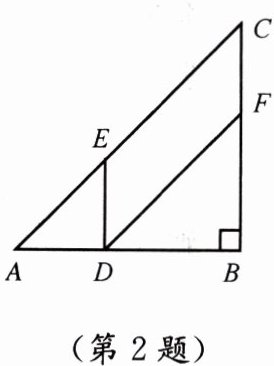

答案:1秒或5秒。
解析:
设点D出发时间为$ t $秒,$ 0 \leq t \leq 6 $。
由题意,$ AD = 2t \, cm $,$ DB = AB - AD = 12 - 2t \, cm $。
方法:面积差法
1. $\triangle ABC$的面积:
$ S_{\triangle ABC} = \frac{1}{2} × AB × BC = \frac{1}{2} × 12 × 12 = 72 \, cm^2 $。
2. $\triangle ADE$的面积:
由于$ DE // BC $,$\triangle ADE \sim \triangle ABC$,相似比为$\frac{AD}{AB} = \frac{2t}{12} = \frac{t}{6}$。
面积比为$\left(\frac{t}{6}\right)^2$,故$ S_{\triangle ADE} = 72 × \left(\frac{t}{6}\right)^2 = 2t^2 $。
3. $\triangle DBF$的面积:
由于$ DF // AC $,$\triangle DBF \sim \triangle ABC$,相似比为$\frac{DB}{AB} = \frac{12 - 2t}{12} = \frac{6 - t}{6}$。
面积比为$\left(\frac{6 - t}{6}\right)^2$,故$ S_{\triangle DBF} = 72 × \left(\frac{6 - t}{6}\right)^2 = 2(6 - t)^2 $。
4. 四边形$ DFCE $的面积:
$ S_{DFCE} = S_{\triangle ABC} - S_{\triangle ADE} - S_{\triangle DBF} $
即$ 72 - 2t^2 - 2(6 - t)^2 = 20 $。
解方程
整理得:
$ 72 - 2t^2 - 2(36 - 12t + t^2) = 20 $
$ 72 - 2t^2 - 72 + 24t - 2t^2 = 20 $
$ -4t^2 + 24t = 20 $
$ t^2 - 6t + 5 = 0 $
解得$ t = 1 $或$ t = 5 $。
结论
点D出发1秒或5秒时,四边形$ DFCE $的面积为$ 20 \, cm^2 $。
由题意,$ AD = 2t \, cm $,$ DB = AB - AD = 12 - 2t \, cm $。
方法:面积差法
1. $\triangle ABC$的面积:
$ S_{\triangle ABC} = \frac{1}{2} × AB × BC = \frac{1}{2} × 12 × 12 = 72 \, cm^2 $。
2. $\triangle ADE$的面积:
由于$ DE // BC $,$\triangle ADE \sim \triangle ABC$,相似比为$\frac{AD}{AB} = \frac{2t}{12} = \frac{t}{6}$。
面积比为$\left(\frac{t}{6}\right)^2$,故$ S_{\triangle ADE} = 72 × \left(\frac{t}{6}\right)^2 = 2t^2 $。
3. $\triangle DBF$的面积:
由于$ DF // AC $,$\triangle DBF \sim \triangle ABC$,相似比为$\frac{DB}{AB} = \frac{12 - 2t}{12} = \frac{6 - t}{6}$。
面积比为$\left(\frac{6 - t}{6}\right)^2$,故$ S_{\triangle DBF} = 72 × \left(\frac{6 - t}{6}\right)^2 = 2(6 - t)^2 $。
4. 四边形$ DFCE $的面积:
$ S_{DFCE} = S_{\triangle ABC} - S_{\triangle ADE} - S_{\triangle DBF} $
即$ 72 - 2t^2 - 2(6 - t)^2 = 20 $。
解方程
整理得:
$ 72 - 2t^2 - 2(36 - 12t + t^2) = 20 $
$ 72 - 2t^2 - 72 + 24t - 2t^2 = 20 $
$ -4t^2 + 24t = 20 $
$ t^2 - 6t + 5 = 0 $
解得$ t = 1 $或$ t = 5 $。
结论
点D出发1秒或5秒时,四边形$ DFCE $的面积为$ 20 \, cm^2 $。