活动一:做一做 想一想
1. 将圆形胶带悬空,转动胶带,你有什么发现?如果把胶带截面看作一个圆,中心点为圆心,请根据你的发现说说圆的相关特性.
2. 完成《数学实验手册》(九年级全一册)“实验 1 旋转、折叠透明纸——验证圆的对称性”的活动,你可以得到哪些结论?尝试用数学语言表述.
1. 将圆形胶带悬空,转动胶带,你有什么发现?如果把胶带截面看作一个圆,中心点为圆心,请根据你的发现说说圆的相关特性.
2. 完成《数学实验手册》(九年级全一册)“实验 1 旋转、折叠透明纸——验证圆的对称性”的活动,你可以得到哪些结论?尝试用数学语言表述.
答案:1. 圆是中心对称图形,圆心是对称中心;2. 圆是中心对称图形,对称中心是圆心;圆是轴对称图形,任意一条直径所在的直线都是它的对称轴。
解析:
1. 发现圆形胶带转动后形状和位置不变,说明圆是中心对称图形,圆心是对称中心。2. 通过旋转、折叠实验可得:圆是中心对称图形,对称中心为圆心;圆是轴对称图形,任意一条直径所在的直线都是对称轴。
活动二:想一想 说一说
认真研读课本内容,说说对下面问题的认识.
(1) 什么是 $1^{\circ}$ 的弧?
(2) 圆心角的度数与它所对弧的度数之间有什么关系?
(3) 度数相等的弧是等弧吗?
认真研读课本内容,说说对下面问题的认识.
(1) 什么是 $1^{\circ}$ 的弧?
(2) 圆心角的度数与它所对弧的度数之间有什么关系?
(3) 度数相等的弧是等弧吗?
答案:(1)把顶点在圆心的周角等分成360份时,每一份这样的弧叫做1°的弧;(2)相等;(3)不是
解析:
(1)把顶点在圆心的周角等分成360份时,每一份的圆心角是1°的角,相应的整个圆也被等分成360份,每一份这样的弧叫做1°的弧。
(2)圆心角的度数与它所对弧的度数相等。
(3)不是,等弧不仅要求度数相等,还要求长度相等(或在同圆或等圆中)。
(2)圆心角的度数与它所对弧的度数相等。
(3)不是,等弧不仅要求度数相等,还要求长度相等(或在同圆或等圆中)。
1. 下列说法中,正确的是 (
A.半圆所对的圆心角是直角
B.度数相等的弧是等弧
C.在同圆或等圆中,如果两条弦相等,那么它们所对的两条弧也相等
D.在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等
D
)A.半圆所对的圆心角是直角
B.度数相等的弧是等弧
C.在同圆或等圆中,如果两条弦相等,那么它们所对的两条弧也相等
D.在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等
答案:D
解析:
A:半圆所对的圆心角是平角,为180°,而不是直角,所以A选项错误;
B:等弧的定义是在同圆或等圆中,能够互相重合的弧,而度数相等的弧不一定能重合,所以B选项错误;
C:在同圆或等圆中,两条弦相等,它们所对的弧可能相等,也可能是优弧和劣弧的关系,所对的弧不一定相等,所以C选项错误;
D:根据圆心角、弧、弦的关系定理,在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等,所以D选项正确。
B:等弧的定义是在同圆或等圆中,能够互相重合的弧,而度数相等的弧不一定能重合,所以B选项错误;
C:在同圆或等圆中,两条弦相等,它们所对的弧可能相等,也可能是优弧和劣弧的关系,所对的弧不一定相等,所以C选项错误;
D:根据圆心角、弧、弦的关系定理,在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等,所以D选项正确。
2. 一条弦把圆分成 $1:3$ 两部分,劣弧所对的圆心角为
90°
.答案:90°
解析:
因为整个圆的圆心角为360°,弦把圆分成1:3两部分,所以劣弧占比为1/(1+3)=1/4,劣弧所对圆心角为360°×1/4=90°。
3. 如图,正方形 $ABCD$ 是 $\odot O$ 的内接四边形,$\angle AOD$ 的度数是
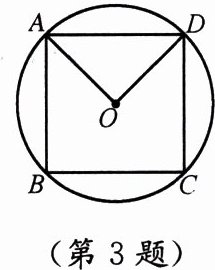
90°
.
答案:90°
解析:
∵正方形ABCD内接于⊙O,∴AB=BC=CD=DA,∴弧AB=弧BC=弧CD=弧DA,∵圆的周角为360°,∴每条弧的度数为360°÷4=90°,∵∠AOD是圆心角,所对弧为弧AD,∴∠AOD=90°
4. 如图,在 $\odot O$ 中,$AB = AC$,$AD$ 是 $\odot O$ 的直径. 试判断弦 $BD$ 与 $CD$ 是否相等,并说明理由.


答案:因为$AB = AC$,
所以$\overset{\frown}{AB} = \overset{\frown}{AC}$。
因为$AD$是$\odot O$的直径,
所以$AD$垂直平分弦$BC$(垂径定理的逆定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧),
即$AD$是$BC$的垂直平分线。
所以$BD = CD$(线段垂直平分线上的点到这条线段两个端点的距离相等)。
所以$\overset{\frown}{AB} = \overset{\frown}{AC}$。
因为$AD$是$\odot O$的直径,
所以$AD$垂直平分弦$BC$(垂径定理的逆定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧),
即$AD$是$BC$的垂直平分线。
所以$BD = CD$(线段垂直平分线上的点到这条线段两个端点的距离相等)。