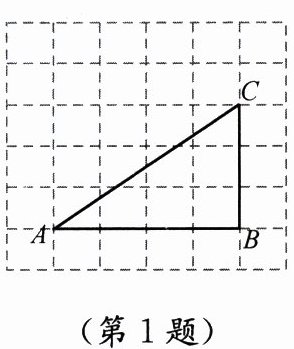
1. 如图,$ \triangle ABC $ 在每个小正方形的边长都为 1 的网格中,点 $ A $、$ B $、$ C $ 均落在格点上,用一个圆形纸片覆盖 $ \triangle ABC $,能够完全覆盖这个三角形的最小圆形纸片的半径是
5/2
.
答案:5/2
解析:
设网格中小正方形边长为1,建立坐标系,得A(0,0),B(4,0),C(4,3)。
计算三边长度:AB=4,BC=3,AC=√[(4-0)²+(3-0)²]=5。
∵AB²+BC²=4²+3²=25=AC²,∴△ABC是直角三角形,斜边AC=5。
直角三角形外接圆半径为斜边一半,故最小覆盖圆半径为AC/2=5/2。
计算三边长度:AB=4,BC=3,AC=√[(4-0)²+(3-0)²]=5。
∵AB²+BC²=4²+3²=25=AC²,∴△ABC是直角三角形,斜边AC=5。
直角三角形外接圆半径为斜边一半,故最小覆盖圆半径为AC/2=5/2。
2. 直角三角形的两条边的长分别为 $ 5 cm $ 和 $ 12 cm $,它的外接圆半径为
6cm或6.5cm
.答案:6cm或6.5cm
解析:
当5cm和12cm为直角边时,斜边为$\sqrt{5^2 + 12^2} = 13$cm,外接圆半径为斜边一半,即$\frac{13}{2} = 6.5$cm;
当12cm为斜边,5cm为直角边时,外接圆半径为斜边一半,即$\frac{12}{2} = 6$cm。
综上,外接圆半径为6cm或6.5cm。
当12cm为斜边,5cm为直角边时,外接圆半径为斜边一半,即$\frac{12}{2} = 6$cm。
综上,外接圆半径为6cm或6.5cm。
3. 根据下列已知条件,不能确定一个圆的是(
A.圆心与半径
B.直径
C.平面上的三个已知点
D.三角形的三个顶点
C
)A.圆心与半径
B.直径
C.平面上的三个已知点
D.三角形的三个顶点
答案:C
解析:
A. 已知圆心和半径可以唯一确定一个圆。
B. 已知直径时,直径的中点为圆心,直径的一半为半径,可以确定一个圆。
C. 平面上的三个已知点,当三点共线时,无法确定一个圆;当三点不共线时,可以确定一个圆。因此,不能保证一定可以确定一个圆。
D. 三角形的三个顶点不共线,可以确定一个唯一的圆(外接圆)。
4. 如图,方格纸上每个小正方形的边长均为 1 个单位长度,点 $ O $、$ A $、$ B $、$ C $ 在格点上,以点 $ O $ 为原点建立平面直角坐标系.
(1) 过 $ A $、$ B $、$ C $ 三点的圆的圆心 $ M $ 的坐标为
(2) 求 $ \odot M $ 的面积(结果保留 $ \pi $).
(1) 过 $ A $、$ B $、$ C $ 三点的圆的圆心 $ M $ 的坐标为
(1,-1)
;(2) 求 $ \odot M $ 的面积(结果保留 $ \pi $).
设圆心$ M(1,-1) $,点$ A(-2,-1) $,则半径$ r = MA = \sqrt{(-2 - 1)^2 + (-1 - (-1))^2} = \sqrt{(-3)^2 + 0^2} = 3 $,面积$ S = \pi r^2 = 9\pi $。
答案:(1) (1,-1)
(2) 设圆心$ M(1,-1) $,点$ A(-2,-1) $,则半径$ r = MA = \sqrt{(-2 - 1)^2 + (-1 - (-1))^2} = \sqrt{(-3)^2 + 0^2} = 3 $,面积$ S = \pi r^2 = 9\pi $。
(2) 设圆心$ M(1,-1) $,点$ A(-2,-1) $,则半径$ r = MA = \sqrt{(-2 - 1)^2 + (-1 - (-1))^2} = \sqrt{(-3)^2 + 0^2} = 3 $,面积$ S = \pi r^2 = 9\pi $。
1. 如图,一只猫发现一只老鼠溜进了鼠洞,该鼠洞只有三个出口 $ A $、$ B $、$ C $,要想同时顾及这三个出口以防老鼠出洞,这只猫最好蹲守在(

A.$ \triangle ABC $ 的三边高线的交点处
B.$ \triangle ABC $ 的三条角平分线的交点处
C.$ \triangle ABC $ 的三边中线的交点处
D.$ \triangle ABC $ 的三边垂直平分线的交点处
D
)
A.$ \triangle ABC $ 的三边高线的交点处
B.$ \triangle ABC $ 的三条角平分线的交点处
C.$ \triangle ABC $ 的三边中线的交点处
D.$ \triangle ABC $ 的三边垂直平分线的交点处
答案:D
解析:
要使猫到三个出口 $A$、$B$、$C$ 的距离相等,才能同时顾及这三个出口。
根据几何性质,三边垂直平分线的交点到三个顶点的距离相等,因此猫应蹲守在 $\triangle ABC$ 的三边垂直平分线的交点处。
根据几何性质,三边垂直平分线的交点到三个顶点的距离相等,因此猫应蹲守在 $\triangle ABC$ 的三边垂直平分线的交点处。
2. 在平面直角坐标系中,点 $ A $、$ B $、$ C $ 的坐标分别为 $ (1, -1) $、$ (-2, 5) $、$ (4, -6) $. 试判断过 $ A $、$ B $、$ C $ 三点能否确定一个圆,并说明你的理由.
答案:设经过点$A(1, -1)$和点$B(-2, 5)$的直线方程为$y = kx + b$。
代入$A(1, -1)$,得:
$-1 = k + b \quad (1)$
代入$B(-2, 5)$,得:
$5 = -2k + b \quad (2)$
从(1)和(2)联立解得:
$k = -2, \quad b = 1$
所以,直线$AB$的方程为$y = -2x + 1$。
将点$C(4, -6)$的坐标代入直线$AB$的方程进行验证:
$-6 = -2 × 4 + 1$
$-6 = -8 + 1$
$-6 \neq -7$
由于上式不成立,所以点$C$不在直线$AB$上。
因为点$C$不在直线$AB$上,所以点$A$、$B$、$C$不共线。
根据确定圆的条件,不共线的三点可以确定一个圆。
所以过$A$、$B$、$C$三点能确定一个圆。
代入$A(1, -1)$,得:
$-1 = k + b \quad (1)$
代入$B(-2, 5)$,得:
$5 = -2k + b \quad (2)$
从(1)和(2)联立解得:
$k = -2, \quad b = 1$
所以,直线$AB$的方程为$y = -2x + 1$。
将点$C(4, -6)$的坐标代入直线$AB$的方程进行验证:
$-6 = -2 × 4 + 1$
$-6 = -8 + 1$
$-6 \neq -7$
由于上式不成立,所以点$C$不在直线$AB$上。
因为点$C$不在直线$AB$上,所以点$A$、$B$、$C$不共线。
根据确定圆的条件,不共线的三点可以确定一个圆。
所以过$A$、$B$、$C$三点能确定一个圆。
3. 如图,在 $ \triangle ABC $ 中,$ AB = AC = 10 $,$ BC = 12 $,求其外接圆的半径.


答案:过A作AD⊥BC于D,∵AB=AC,∴AD垂直平分BC,D为BC中点。
BC=12,∴BD=6。
在Rt△ABD中,AB=10,BD=6,由勾股定理得AD=√(AB²-BD²)=√(10²-6²)=8。
设外接圆半径为R,圆心O在AD上,OA=OB=R,设OD=x,则OD=AD-OA=8-R。
在Rt△OBD中,OB²=OD²+BD²,即R²=(8-R)²+6²。
展开得R²=64-16R+R²+36,化简得16R=100,解得R=25/4。
25/4
BC=12,∴BD=6。
在Rt△ABD中,AB=10,BD=6,由勾股定理得AD=√(AB²-BD²)=√(10²-6²)=8。
设外接圆半径为R,圆心O在AD上,OA=OB=R,设OD=x,则OD=AD-OA=8-R。
在Rt△OBD中,OB²=OD²+BD²,即R²=(8-R)²+6²。
展开得R²=64-16R+R²+36,化简得16R=100,解得R=25/4。
25/4