1. 如图2-5,在足球比赛中,甲带球向对方球门PQ进攻,当他带球冲到点A时,同样乙已经助攻冲到点B,丙助攻到点C。有三种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门;第三种是甲将球传给丙,由丙射门。仅从射门角度大小考虑,应选择第
]
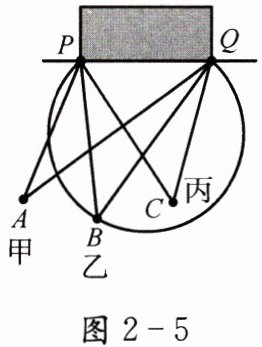
第三种
种射门方式。]

答案:第三种
解析:
射门角度为射门点对球门PQ的张角,即∠PAQ、∠PBQ、∠PCQ。根据圆周角性质及圆内、外角大小关系:对于弦PQ,圆内角大于同弧所对圆周角,圆周角大于圆外角。假设点B在过P、Q的圆上(圆周角),点C在圆内(圆内角),点A在圆外(圆外角),则∠PCQ>∠PBQ>∠PAQ,故丙射门角度最大。
2. 如图2-6,AB为⊙O的直径,∠BOC、∠BAC分别是⌢BC所对的圆心角、圆周角,直接写出图2-6①、图2-6②中∠BAC的度数,并结合图2-6③写出计算过程。
]

]

答案:①45°
②60°
③∵∠BOC是⌢BC所对的圆心角,∠BAC是⌢BC所对的圆周角,
∴∠BAC=1/2∠BOC=1/2n°
②60°
③∵∠BOC是⌢BC所对的圆心角,∠BAC是⌢BC所对的圆周角,
∴∠BAC=1/2∠BOC=1/2n°
1. 如图2-7,点B、C在⊙O上。
⌢BC所对的圆心角有
]

⌢BC所对的圆心角有
1
个,⌢BC所对的圆周角有无数
个。]

答案:1;无数
解析:
在同圆中,一条弧所对的圆心角只有1个,即∠BOC;一条弧所对的圆周角有无数个,这些圆周角的顶点分布在弧BC所对的优弧和劣弧上(除B、C两点外)。
2. 在⊙O中画出⌢BC所对的圆心角和圆周角。所画的圆周角与圆心O有哪几种不同的位置关系?请分别画出对应的图形。
3. 根据第2题所画的不同位置关系,你能探索出同弧所对的圆周角和圆心角的数量关系吗?
3. 根据第2题所画的不同位置关系,你能探索出同弧所对的圆周角和圆心角的数量关系吗?
答案:2.
图1(圆心在圆周角内部):
画⊙O,标出弧BC。
圆心角:∠BOC(顶点O,边B、C)。
圆周角:∠BAC(顶点A在⊙O上,边B、C)。
图2(圆心在圆周角一侧):
画⊙O,标出弧BC。
圆心角:∠BOC。
圆周角:∠BAC(顶点A在⊙O上,OA与OB重合时为一种情况,此时圆周角一侧边与圆心角一边重合)。
图3(圆心在圆周角外部):
画⊙O,标出弧BC。
圆心角:∠BOC。
圆周角:∠BAC(顶点A在⊙O上,O在∠BAC外部)。
(实际作图应使用圆规和量角器规范画出,此处为文字描述)。
3.
根据所画图形,同弧BC所对的圆周角∠BAC与圆心角∠BOC的数量关系为:
$∠BAC = \frac{1}{2}∠BOC$。
图1(圆心在圆周角内部):
画⊙O,标出弧BC。
圆心角:∠BOC(顶点O,边B、C)。
圆周角:∠BAC(顶点A在⊙O上,边B、C)。
图2(圆心在圆周角一侧):
画⊙O,标出弧BC。
圆心角:∠BOC。
圆周角:∠BAC(顶点A在⊙O上,OA与OB重合时为一种情况,此时圆周角一侧边与圆心角一边重合)。
图3(圆心在圆周角外部):
画⊙O,标出弧BC。
圆心角:∠BOC。
圆周角:∠BAC(顶点A在⊙O上,O在∠BAC外部)。
(实际作图应使用圆规和量角器规范画出,此处为文字描述)。
3.
根据所画图形,同弧BC所对的圆周角∠BAC与圆心角∠BOC的数量关系为:
$∠BAC = \frac{1}{2}∠BOC$。