1. 下列说法中,正确的是(
A.顶点在圆周上的角叫做圆周角
B.圆周角等于圆心角的一半
C.同弧所对的圆周角相等
D.等弦所对的圆周角相等
C
)A.顶点在圆周上的角叫做圆周角
B.圆周角等于圆心角的一半
C.同弧所对的圆周角相等
D.等弦所对的圆周角相等
答案:C
解析:
A. 圆周角的定义是顶点在圆上,并且两边都与圆相交的角,仅仅顶点在圆周上不够,故A错误;
B. 在同弧或等弧所对的圆周角和圆心角中,圆周角等于圆心角的一半,缺少前提条件,故B错误;
C. 根据圆周角定理,同弧所对的圆周角相等,故C正确;
D. 等弦所对的圆周角可能相等也可能互补,故D错误。
B. 在同弧或等弧所对的圆周角和圆心角中,圆周角等于圆心角的一半,缺少前提条件,故B错误;
C. 根据圆周角定理,同弧所对的圆周角相等,故C正确;
D. 等弦所对的圆周角可能相等也可能互补,故D错误。
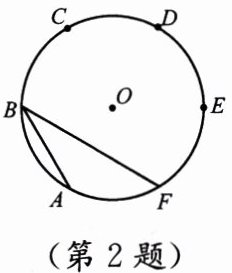
2. 如图,A、B、C、D、E、F是⊙O的六等分点,∠ABF等于(
A.22.5°
B.30°
C.45°
D.60°
]
B
)
A.22.5°
B.30°
C.45°
D.60°
]
答案:B
解析:
连接OA、OF。因为A、B、C、D、E、F是⊙O的六等分点,所以每段弧的度数为360°÷6=60°,即弧AF的度数为60°。∠ABF是圆周角,它所对的弧是弧AF,根据圆周角定理,圆周角的度数等于它所对弧的度数的一半,所以∠ABF=60°÷2=30°。
3. 如图,在⊙O中,AC//OB,∠BAO= 25°,则∠BOC的度数为(

A.25°
B.50°
C.60°
D.80°
]
B
)
A.25°
B.50°
C.60°
D.80°
]
答案:B
解析:
∵OA=OB,∠BAO=25°,∴∠ABO=∠BAO=25°.
∵AC//OB,∴∠CAB=∠ABO=25°,∠CAO=∠BAO+∠CAB=50°.
∵OA=OC,∴∠ACO=∠CAO=50°,∠AOC=180°-50°-50°=80°.
∵AC//OB,∴∠BOC=∠ACO=50°.
∵AC//OB,∴∠CAB=∠ABO=25°,∠CAO=∠BAO+∠CAB=50°.
∵OA=OC,∴∠ACO=∠CAO=50°,∠AOC=180°-50°-50°=80°.
∵AC//OB,∴∠BOC=∠ACO=50°.
4. 如图,AB、AC为⊙O的两条弦,延长CA到点D,使AD= AB,∠ADB= 35°,求∠BOC的度数。
]

]

答案:设$\angle ABD = x$,
因为$AD = AB$,
所以$\angle ABD = \angle ADB=35^\circ$(等边对等角),
则$\angle BAC =\angle ABD + \angle ADB=70^\circ$(三角形外角等于不相邻两内角和)。
因为$\angle BAC$是圆周角,$\angle BOC$是圆心角,且它们所对的弧都是$\overset{\frown} {BC}$,
根据同弧所对圆心角是圆周角的两倍,
所以$\angle BOC = 2\angle BAC = 140^{\circ}$。
综上,$\angle BOC$的度数为$140^{\circ}$。
因为$AD = AB$,
所以$\angle ABD = \angle ADB=35^\circ$(等边对等角),
则$\angle BAC =\angle ABD + \angle ADB=70^\circ$(三角形外角等于不相邻两内角和)。
因为$\angle BAC$是圆周角,$\angle BOC$是圆心角,且它们所对的弧都是$\overset{\frown} {BC}$,
根据同弧所对圆心角是圆周角的两倍,
所以$\angle BOC = 2\angle BAC = 140^{\circ}$。
综上,$\angle BOC$的度数为$140^{\circ}$。
1. 如图,⊙O的直径CD过弦EF的中点G,∠EOD= 40°,则∠FCD=
]

20°
。]

答案:20°
解析:
∵CD是⊙O的直径,G是EF的中点,∴CD⊥EF,$\widehat{ED}=\widehat{FD}$(垂径定理)。∵∠EOD=40°,∴∠FOD=∠EOD=40°。∴∠COD=180°,∠COF=∠COD - ∠FOD=180° - 40°=140°。∵OC=OF(半径相等),∴∠FCD=∠OFC。在△COF中,∠FCD + ∠OFC + ∠COF=180°,即2∠FCD + 140°=180°,解得∠FCD=20°。
2. 如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB= 45°,则四边形MANB面积的最大值是______
]

4√2
。]

答案:4√2
解析:
连接OA、OB,∵∠AMB=45°,∴∠AOB=2∠AMB=90°(圆周角定理)。在Rt△AOB中,OA=OB=2,∴AB=√(OA²+OB²)=√(2²+2²)=2√2。
四边形MANB面积S=S△MAB+S△NAB=(1/2)AB·h₁+(1/2)AB·h₂=(1/2)AB(h₁+h₂),其中h₁、h₂分别为M、N到AB的距离。
圆心O到AB的距离d=√(OA²-(AB/2)²)=√(4-2)=√2。M、N在AB异侧,h₁最大值为d+2=√2+2,h₂最大值为2-d=2-√2(h₂=|y_N|=2-d)。
h₁+h₂最大值=(√2+2)+(2-√2)=4。∴S最大值=(1/2)×2√2×4=4√2。
四边形MANB面积S=S△MAB+S△NAB=(1/2)AB·h₁+(1/2)AB·h₂=(1/2)AB(h₁+h₂),其中h₁、h₂分别为M、N到AB的距离。
圆心O到AB的距离d=√(OA²-(AB/2)²)=√(4-2)=√2。M、N在AB异侧,h₁最大值为d+2=√2+2,h₂最大值为2-d=2-√2(h₂=|y_N|=2-d)。
h₁+h₂最大值=(√2+2)+(2-√2)=4。∴S最大值=(1/2)×2√2×4=4√2。
3. 如图,△ABC内接于⊙O,AB= AC,D是⌢AC上一点,连接BD,E是BD上的一点,且BE= CD。求证:∠AED= ∠ADE。
]

]

答案:证明:∵AB=AC,∴弧AB=弧AC,∴∠ABC=∠ACB(等弦对等弧,等弧对等圆周角)。
∵∠ABD与∠ACD均为弧AD所对的圆周角,∴∠ABD=∠ACD(同弧所对圆周角相等)。
在△ABE和△ACD中,
AB=AC(已知),
∠ABE=∠ACD(已证),
BE=CD(已知),
∴△ABE≌△ACD(SAS)。
∴AE=AD(全等三角形对应边相等)。
∴∠AED=∠ADE(等边对等角)。
∵∠ABD与∠ACD均为弧AD所对的圆周角,∴∠ABD=∠ACD(同弧所对圆周角相等)。
在△ABE和△ACD中,
AB=AC(已知),
∠ABE=∠ACD(已证),
BE=CD(已知),
∴△ABE≌△ACD(SAS)。
∴AE=AD(全等三角形对应边相等)。
∴∠AED=∠ADE(等边对等角)。