2. 如图,AB 是⊙O 的直径,∠ABC = 28°,则∠BDC =

62
°。
答案:62
解析:
∵AB是⊙O的直径,∴∠ACB=90°。∵∠ABC=28°,∴∠BAC=90°-28°=62°。∵∠BDC与∠BAC所对的弧都是弧BC,∴∠BDC=∠BAC=62°。
3. 如图,□ABCD 的顶点 A、B、D 在⊙O 上,顶点 C 在⊙O 的直径 BE 上,∠ADC = 70°,连接 AE,则∠AEB 的度数为

20°
。
答案:20°
解析:
∵四边形ABCD是平行四边形,∠ADC=70°,
∴∠ABC=∠ADC=70°(平行四边形对角相等)。
∵BE是⊙O的直径,点A在⊙O上,
∴∠BAE=90°(直径所对的圆周角是直角)。
∵点C在BE上,∴∠ABE=∠ABC=70°。
在Rt△ABE中,∠AEB=90°-∠ABE=90°-70°=20°。
4. 以 O 为中心点的量角器与含 45°角的三角板 ABC 按如图方式摆放,量角器的零刻度线与斜边 AB 重合。点 D 为斜边 AB 上一点,作射线 CD 交弧 AB 于点 E,如果点 E 所对应的量角器刻度为 52°,那么∠BCD 的度数为(

A.52°
B.60°
C.64°
D.69°
C
)
A.52°
B.60°
C.64°
D.69°
答案:C
解析:
连接OE,量角器中心为O,AB为直径,故OA=OB=OE。点E对应刻度52°,即圆心角∠BOE=52°。
弧BE所对圆周角∠BCE=1/2∠BOE=26°(圆周角定理)。
△ABC为等腰直角三角形,∠ACB=90°。
∠BCD=∠ACB - ∠BCE=90° - 26°=64°。
弧BE所对圆周角∠BCE=1/2∠BOE=26°(圆周角定理)。
△ABC为等腰直角三角形,∠ACB=90°。
∠BCD=∠ACB - ∠BCE=90° - 26°=64°。
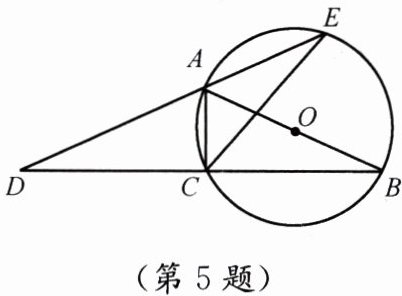
5. 如图,AB 为⊙O 的直径,点 C 在⊙O 上,延长 BC 到点 D,使 DC = CB,延长 DA,交⊙O 于点 E,连接 AC、CE。
(1)试说明∠B = ∠D;
(2)若 AB = 4,BC - AC = 2,求 CE 的长。
(1)试说明∠B = ∠D;
(2)若 AB = 4,BC - AC = 2,求 CE 的长。

答案:(1)见解析;(2)CE=√7+1。
解析:
(1)∵AB是⊙O直径,∴∠ACB=90°(直径所对圆周角是直角)。
∵D在BC延长线上,∴∠ACD=180°-∠ACB=90°。
∵DC=CB,∠ACD=∠ACB=90°,AC=AC,
∴△ACD≌△ACB(SAS),∴∠D=∠B。
(2)设AC=x,BC=y,∵BC-AC=2,∴y=x+2。
∵AB是直径,AB=4,∴∠ACB=90°,∴AC²+BC²=AB²,即x²+y²=16。
将y=x+2代入x²+y²=16,得x²+(x+2)²=16,
整理得2x²+4x-12=0,即x²+2x-6=0,
解得x=-1±√7,∵x>0,∴x=√7-1,
∴y=x+2=√7+1,即BC=√7+1。
∵∠B=∠D(已证),∠B=∠AEC(同弧AC所对圆周角相等),
∴∠D=∠AEC=∠DEC,∴CE=CD。
∵DC=CB,∴CE=CB=√7+1。
∵D在BC延长线上,∴∠ACD=180°-∠ACB=90°。
∵DC=CB,∠ACD=∠ACB=90°,AC=AC,
∴△ACD≌△ACB(SAS),∴∠D=∠B。
(2)设AC=x,BC=y,∵BC-AC=2,∴y=x+2。
∵AB是直径,AB=4,∴∠ACB=90°,∴AC²+BC²=AB²,即x²+y²=16。
将y=x+2代入x²+y²=16,得x²+(x+2)²=16,
整理得2x²+4x-12=0,即x²+2x-6=0,
解得x=-1±√7,∵x>0,∴x=√7-1,
∴y=x+2=√7+1,即BC=√7+1。
∵∠B=∠D(已证),∠B=∠AEC(同弧AC所对圆周角相等),
∴∠D=∠AEC=∠DEC,∴CE=CD。
∵DC=CB,∴CE=CB=√7+1。
1. 如图,⊙A 的半径为 5,BC、DE 为两条弦。已知 DE = 6,∠BAC + ∠EAD = 180°,则圆心 A 到 BC 的距离等于

3
。
答案:3
解析:
过点A作AM⊥BC于M,AN⊥DE于N,连接AB、AD。
由垂径定理得:BM=CM,DN=EN=DE/2=3。
在Rt△ADN中,AD=5,DN=3,∴AN²=AD²-DN²=5²-3²=16,AN=4。
设∠BAC=α,则∠EAD=180°-α,∠BAM=α/2,∠DAN=(180°-α)/2=90°-α/2。
在Rt△ABM中,cos(α/2)=AM/AB=AM/5;在Rt△ADN中,cos(90°-α/2)=AN/AD=4/5,即sin(α/2)=4/5。
∵sin²(α/2)+cos²(α/2)=1,∴(4/5)²+(AM/5)²=1,解得AM=3。
由垂径定理得:BM=CM,DN=EN=DE/2=3。
在Rt△ADN中,AD=5,DN=3,∴AN²=AD²-DN²=5²-3²=16,AN=4。
设∠BAC=α,则∠EAD=180°-α,∠BAM=α/2,∠DAN=(180°-α)/2=90°-α/2。
在Rt△ABM中,cos(α/2)=AM/AB=AM/5;在Rt△ADN中,cos(90°-α/2)=AN/AD=4/5,即sin(α/2)=4/5。
∵sin²(α/2)+cos²(α/2)=1,∴(4/5)²+(AM/5)²=1,解得AM=3。
2. 如图,在⊙O 中,AB 是直径,BC 是弦,P 是$\overset{\frown}{BC}$上任意一点。若 AB = 5,BC = 3,则 AP 的长不可能为(

A.3
B.4
C.$\frac{9}{2}$
D.5
A
)
A.3
B.4
C.$\frac{9}{2}$
D.5
答案:A
解析:
连接AC,∵AB是直径,∴∠ACB=90°。在Rt△ABC中,AB=5,BC=3,由勾股定理得AC=√(AB²-BC²)=√(25-9)=4。∵P是$\overset{\frown}{BC}$上任意一点,当P与C重合时,AP=AC=4;当P与B重合时,AP=AB=5。∴AP长度范围为4≤AP≤5。选项中3不在此范围,故选A。
3. 如图,在四边形 ABCD 中,∠ABC = ∠ADC = 90°,E 为对角线 AC 的中点,连接 BE、ED、BD。若∠BAD = 58°,则∠EBD 的度数为

32°
。
答案:32°
解析:
∵∠ABC=∠ADC=90°,E为AC中点,∴BE=AE=DE=AC/2(直角三角形斜边中线等于斜边一半),故A、B、C、D四点共圆,E为圆心,AC为直径。∠BAD=58°,则弧BD所对圆周角为∠BAD=58°,所对圆心角∠BED=2∠BAD=116°。∵BE=DE,∴△BED为等腰三角形,∠EBD=(180°-∠BED)/2=(180°-116°)/2=32°。