1. 如图2-11,△ABC称为⊙O的
内接
三角形,⊙O称为△ABC的外接
圆.答案:内接,外接
解析:
根据三角形与圆的关系,如果三角形的三个顶点都在圆上,这个三角形叫做圆的内接三角形,这个圆叫做三角形的外接圆。
2. 如图2-11,若$\overgroup{BC}的度数为100^{\circ}$,则∠BOC=
100°
,∠A=50°
.答案:100°,50°
解析:
因为圆心角的度数等于它所对弧的度数,所以∠BOC=100°;又因为同弧所对的圆周角等于圆心角的一半,所以∠A=100°÷2=50°。
3. 如图2-12,在四边形ABCD中,∠B与∠1互补,∠2= $60^{\circ}$,则∠1=
120°
,∠B= 60°
.答案:120°,60°
解析:
由图2-12可知,∠1与∠2是邻补角,所以∠1+∠2=180°。因为∠2=60°,所以∠1=180°-∠2=180°-60°=120°。又因为∠B与∠1互补,即∠B+∠1=180°,所以∠B=180°-∠1=180°-120°=60°。
1. 如图2-13,四边形ABCD的各顶点都在⊙O上,四边形ABCD是⊙O的
内接
四边形,⊙O是四边形ABCD的外接
圆.
答案:内接;外接
解析:
如果一个四边形的所有顶点都在同一个圆上,这个四边形叫做圆内接四边形,这个圆叫做这个四边形的外接圆。由图可知四边形ABCD的各顶点都在⊙O上,所以四边形ABCD是⊙O的内接四边形,⊙O是四边形ABCD的外接圆。
2. 如图2-13,在⊙O的内接四边形ABCD中,
(1)∠A所对的弧是哪条弧?∠C所对的弧是哪条弧?
(2)∠A与∠C所对的两条弧的度数之和是多少?由此你发现,∠A与∠C有怎样的数量关系?∠B与∠D呢?
(1)∠A所对的弧是哪条弧?∠C所对的弧是哪条弧?
(2)∠A与∠C所对的两条弧的度数之和是多少?由此你发现,∠A与∠C有怎样的数量关系?∠B与∠D呢?
答案:(1)∠A所对的弧是弧$BCD$(或弧$BC,CD$组成的弧);∠C所对的弧是弧$BAD$(或弧$BA,AD$组成的弧)。
(2)∠A与∠C所对的两条弧的度数之和是$360{^\circ}$;
根据圆周角定理,同弧所对的圆周角相等,且等于这条弧所对圆心角的一半,而一条弧所对的圆心角为这条弧的度数,所以∠A与∠C的和为$360{^\circ} ÷ 2 = 180{^\circ}$;
同理,∠B与∠D的和也为$180{^\circ}$。
即:$\angle A + \angle C = 180{^\circ}$,$\angle B + \angle D = 180{^\circ}$。
(2)∠A与∠C所对的两条弧的度数之和是$360{^\circ}$;
根据圆周角定理,同弧所对的圆周角相等,且等于这条弧所对圆心角的一半,而一条弧所对的圆心角为这条弧的度数,所以∠A与∠C的和为$360{^\circ} ÷ 2 = 180{^\circ}$;
同理,∠B与∠D的和也为$180{^\circ}$。
即:$\angle A + \angle C = 180{^\circ}$,$\angle B + \angle D = 180{^\circ}$。
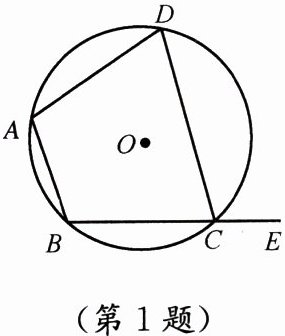
1. 如图,四边形ABCD内接于⊙O,E是BC延长线上一点,若∠BAD= $105^{\circ}$,则∠DCE的度数是
105
°.答案:105
解析:
∵四边形ABCD内接于⊙O,∴∠BAD + ∠BCD = 180°(圆内接四边形的对角互补)。∵∠BAD = 105°,∴∠BCD = 180° - 105° = 75°。∵∠DCE + ∠BCD = 180°(平角定义),∴∠DCE = 180° - 75° = 105°。