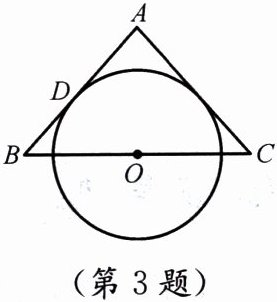
3. 如图,在$\triangle ABC$中,$AB = AC$,以$BC的中点O为圆心作\odot O$,使$\odot O与AB$相切,切点为$D$. 求证:$AC是\odot O$的切线.

答案:证明:
1. 过点$ O $作$ OE \perp AC $,垂足为$ E $,连接$ OA $,$ OD $。
2. 因为$ AB $是$ \odot O $的切线,$ D $为切点,所以$ OD \perp AB $(切线的性质),即$ \angle ODA = 90^\circ $。
3. 因为$ AB = AC $,$ O $是$ BC $中点,所以$ AO $平分$ \angle BAC $(等腰三角形三线合一),即$ \angle OAD = \angle OAE $。
4. 在$ \triangle AOD $和$ \triangle AOE $中:
$ \begin{cases} \angle OAD = \angle OAE, \\ \angle ADO = \angle AEO = 90^\circ, \\ AO = AO, \end{cases} $
所以$ \triangle AOD \cong \triangle AOE \, (AAS) $。
5. 因此$ OD = OE $(全等三角形对应边相等)。
6. 因为$ OD $是$ \odot O $的半径,所以$ OE = OD $也是$ \odot O $的半径。
7. 又因为$ OE \perp AC $,所以$ AC $是$ \odot O $的切线(切线的判定定理)。
结论: $ AC $是$ \odot O $的切线。
1. 过点$ O $作$ OE \perp AC $,垂足为$ E $,连接$ OA $,$ OD $。
2. 因为$ AB $是$ \odot O $的切线,$ D $为切点,所以$ OD \perp AB $(切线的性质),即$ \angle ODA = 90^\circ $。
3. 因为$ AB = AC $,$ O $是$ BC $中点,所以$ AO $平分$ \angle BAC $(等腰三角形三线合一),即$ \angle OAD = \angle OAE $。
4. 在$ \triangle AOD $和$ \triangle AOE $中:
$ \begin{cases} \angle OAD = \angle OAE, \\ \angle ADO = \angle AEO = 90^\circ, \\ AO = AO, \end{cases} $
所以$ \triangle AOD \cong \triangle AOE \, (AAS) $。
5. 因此$ OD = OE $(全等三角形对应边相等)。
6. 因为$ OD $是$ \odot O $的半径,所以$ OE = OD $也是$ \odot O $的半径。
7. 又因为$ OE \perp AC $,所以$ AC $是$ \odot O $的切线(切线的判定定理)。
结论: $ AC $是$ \odot O $的切线。
4. 如图,$AB是\odot O$的直径,$BC与\odot O相切于点B$,弦$AD// OC$. 求证:$DC是\odot O$的切线.


答案:连接$OD$。
由于$AD// OC$,
根据平行线的性质,得到:
$\angle A = \angle BOC$(两直线平行,同位角相等)
$\angle ADO = \angle DOC$(两直线平行,内错角相等)。
由于$OA = OD$(半径相等),
根据等腰三角形的性质,得到:
$\angle A = \angle ADO$。
由上述两个结论,可以得到:
$\angle BOC = \angle DOC$。
在$\triangle BOC$和$\triangle DOC$中,
由于$OB = OD$(半径相等),
$\angle BOC = \angle DOC$,且$OC = OC$(公共边),
根据$SAS$三角形全等的判定,得到:
$\triangle BOC \cong \triangle DOC$。
由于全等三角形的对应角相等,
所以$\angle OBC = \angle ODC$。
又因为$BC$是$\odot O$的切线,
根据切线的性质,得到:
$\angle OBC = 90^\circ$。
因此,$\angle ODC = 90^\circ$,
即$OD \perp DC$。
由于$OD$是$\odot O$的半径,
根据切线的判定定理,得到:
$DC$是$\odot O$的切线。
由于$AD// OC$,
根据平行线的性质,得到:
$\angle A = \angle BOC$(两直线平行,同位角相等)
$\angle ADO = \angle DOC$(两直线平行,内错角相等)。
由于$OA = OD$(半径相等),
根据等腰三角形的性质,得到:
$\angle A = \angle ADO$。
由上述两个结论,可以得到:
$\angle BOC = \angle DOC$。
在$\triangle BOC$和$\triangle DOC$中,
由于$OB = OD$(半径相等),
$\angle BOC = \angle DOC$,且$OC = OC$(公共边),
根据$SAS$三角形全等的判定,得到:
$\triangle BOC \cong \triangle DOC$。
由于全等三角形的对应角相等,
所以$\angle OBC = \angle ODC$。
又因为$BC$是$\odot O$的切线,
根据切线的性质,得到:
$\angle OBC = 90^\circ$。
因此,$\angle ODC = 90^\circ$,
即$OD \perp DC$。
由于$OD$是$\odot O$的半径,
根据切线的判定定理,得到:
$DC$是$\odot O$的切线。
1. 如图,直线$BC切\odot O于点C$,$DE是\odot O$的直径,$\angle A= \angle B = 26^{\circ}$,则$\angle DEC= $

38°
.
答案:38°
解析:
连接OC,∵BC切⊙O于点C,∴OC⊥BC,∠OCB=90°。在△ABC中,∠A=∠B=26°,∴∠ACB=180°-26°-26°=128°。∵∠ACB=128°,∠OCB=90°,∴∠ACO=∠ACB-∠OCB=128°-90°=38°。∵DE是直径,O为圆心,∴OC=OE,△OCE为等腰三角形,∠OCE=∠OEC。又∵点E在直线AC上,∴∠OCE=∠ACO=38°,∴∠DEC=∠OEC=∠OCE=38°。
2. 如图,正方形$ABCD$的边长为 8,$M是边AB$的中点,$P是边BC$上的动点,连接$PM$,以点$P$为圆心,$PM长为半径作\odot P$. 当$\odot P与正方形ABCD$的边相切时,$BP$的长为

3或4√3
.
答案:3或4√3
解析:
设BP=x,以B为原点,BC为x轴,BA为y轴建立坐标系,则B(0,0),C(8,0),A(0,8),M(0,4),P(x,0)。圆P半径PM=√(x²+16)。
与CD边(x=8)相切:圆心到CD距离8-x=√(x²+16),解得x=3。
与AD边(y=8)相切:圆心到AD距离8=√(x²+16),解得x=4√3。
与CD边(x=8)相切:圆心到CD距离8-x=√(x²+16),解得x=3。
与AD边(y=8)相切:圆心到AD距离8=√(x²+16),解得x=4√3。
3. 如图,$AB是\odot O$的直径,$ED与\odot O相切于点C$,$AD与\odot O相交于点A$、$F$,$AC平分\angle BAD$,连接$BF$.
(1) 求证:$AD\perp ED$;
(2) 若$CD = 4$,$AF = 2$,求$\odot O$的半径.

(1) 求证:$AD\perp ED$;
(2) 若$CD = 4$,$AF = 2$,求$\odot O$的半径.

答案:(1) 证明见上;(2) √17
解析:
(1) 连接OC,
∵ED与⊙O相切于点C,∴OC⊥ED(切线垂直于过切点的半径),即∠OCE=90°.
∵AC平分∠BAD,∴∠BAC=∠CAD.
∵OA=OC,∴∠OAC=∠OCA(等边对等角).
又∠OAC=∠BAC,∴∠OCA=∠CAD(等量代换).
∴OC//AD(内错角相等,两直线平行).
∵OC⊥ED,∴AD⊥ED(两平行线中一条垂直于第三条直线,另一条也垂直于第三条直线).
(2) 设⊙O半径为r,连接OC,过O作OM⊥AD于M.
∵AD⊥ED,OC⊥ED,OM⊥AD,∴四边形OCDM为矩形,∴OM=CD=4,OC=MD=r.
∵OM⊥AD,∴M为AF中点(垂径定理),AF=2,∴AM=MF=1.
在Rt△OAM中,OA²=AM²+OM²,即r²=1²+4²=1+16=17,∴r=√17(负值舍去).
∵ED与⊙O相切于点C,∴OC⊥ED(切线垂直于过切点的半径),即∠OCE=90°.
∵AC平分∠BAD,∴∠BAC=∠CAD.
∵OA=OC,∴∠OAC=∠OCA(等边对等角).
又∠OAC=∠BAC,∴∠OCA=∠CAD(等量代换).
∴OC//AD(内错角相等,两直线平行).
∵OC⊥ED,∴AD⊥ED(两平行线中一条垂直于第三条直线,另一条也垂直于第三条直线).
(2) 设⊙O半径为r,连接OC,过O作OM⊥AD于M.
∵AD⊥ED,OC⊥ED,OM⊥AD,∴四边形OCDM为矩形,∴OM=CD=4,OC=MD=r.
∵OM⊥AD,∴M为AF中点(垂径定理),AF=2,∴AM=MF=1.
在Rt△OAM中,OA²=AM²+OM²,即r²=1²+4²=1+16=17,∴r=√17(负值舍去).