1. 下列命题中,真命题有(
① 任意一个三角形一定有一个外接圆,并且只有一个外接圆;② 任意一个圆一定有一个内接三角形,并且只有一个内接三角形;③ 任意一个三角形一定有一个内切圆,并且只有一个内切圆;④ 任意一个圆一定有一个外切三角形,并且只有一个外切三角形.
A.1 个
B.2 个
C.3 个
D.4 个
B
)① 任意一个三角形一定有一个外接圆,并且只有一个外接圆;② 任意一个圆一定有一个内接三角形,并且只有一个内接三角形;③ 任意一个三角形一定有一个内切圆,并且只有一个内切圆;④ 任意一个圆一定有一个外切三角形,并且只有一个外切三角形.
A.1 个
B.2 个
C.3 个
D.4 个
答案:B
解析:
① 根据三角形外接圆的定义和性质,每个三角形都有且仅有一个外接圆,因为三角形的三个顶点不在同一条直线上,所以可以确定唯一的圆经过这三个点,故正确;
② 圆的内接三角形有无数个,因为可以在圆上任意选择三个点作为三角形的顶点,故错误;
③ 根据三角形内切圆的定义和性质,每个三角形都有且仅有一个内切圆,该圆与三角形的三边都相切,故正确;
④ 圆的外切三角形也有无数个,因为可以在圆外选择任意三个点,只要满足这三个点与圆相切的条件即可构成外切三角形,故错误。
综上所述,真命题有2个。
② 圆的内接三角形有无数个,因为可以在圆上任意选择三个点作为三角形的顶点,故错误;
③ 根据三角形内切圆的定义和性质,每个三角形都有且仅有一个内切圆,该圆与三角形的三边都相切,故正确;
④ 圆的外切三角形也有无数个,因为可以在圆外选择任意三个点,只要满足这三个点与圆相切的条件即可构成外切三角形,故错误。
综上所述,真命题有2个。
2. 若 $ \triangle ABC $ 的内切圆半径为 $ r $,$ \triangle ABC $ 的周长为 $ l $,则 $ \triangle ABC $ 的面积为
$\frac{1}{2}lr$
.答案:$\frac{1}{2}lr$
解析:
连接内切圆圆心与三角形三个顶点,将△ABC分割为三个小三角形,其面积分别为$\frac{1}{2}AB \cdot r$、$\frac{1}{2}BC \cdot r$、$\frac{1}{2}AC \cdot r$。△ABC的面积为这三个小三角形面积之和,即$\frac{1}{2}(AB + BC + AC) \cdot r$。因为△ABC的周长$l = AB + BC + AC$,所以面积为$\frac{1}{2}lr$。
3. 在 $ \triangle ABC $ 中,$ \angle A = 72^{\circ} $,若 $ I $ 是 $ \triangle ABC $ 的内心,则 $ \angle BIC = $
$126^{\circ}$
;若 $ I $ 是 $ \triangle ABC $ 的外心,则 $ \angle BIC = $ $144^{\circ}$
.答案:$126^{\circ}$;$144^{\circ}$(按照题目顺序分别填写答案)
解析:
1.当$I$是$\triangle ABC$的内心时:
因为$I$是$\triangle ABC$的内心,则$BI$、$CI$分别是$\angle ABC$、$\angle ACB$的角平分线。
在$\triangle ABC$中,$\angle A = 72^{\circ}$,根据三角形内角和为$180^{\circ}$,可得$\angle ABC+\angle ACB = 180^{\circ}-\angle A=180 - 72 = 108^{\circ}$。
所以$\angle IBC+\angle ICB=\frac{1}{2}(\angle ABC + \angle ACB)=\frac{1}{2}×108^{\circ}=54^{\circ}$。
在$\triangle BIC$中,根据三角形内角和为$180^{\circ}$,可得$\angle BIC = 180^{\circ}-(\angle IBC+\angle ICB)=180 - 54 = 126^{\circ}$。
2.当$I$是$\triangle ABC$的外心时:
根据圆周角定理,同弧所对的圆周角是圆心角的一半。
因为$I$是$\triangle ABC$的外心,所以$\angle BIC$是圆心角,$\angle A$是圆周角,且它们所对的弧都是$\overset{\frown}{BC}$,则$\angle BIC = 2\angle A=2×72^{\circ}=144^{\circ}$。
因为$I$是$\triangle ABC$的内心,则$BI$、$CI$分别是$\angle ABC$、$\angle ACB$的角平分线。
在$\triangle ABC$中,$\angle A = 72^{\circ}$,根据三角形内角和为$180^{\circ}$,可得$\angle ABC+\angle ACB = 180^{\circ}-\angle A=180 - 72 = 108^{\circ}$。
所以$\angle IBC+\angle ICB=\frac{1}{2}(\angle ABC + \angle ACB)=\frac{1}{2}×108^{\circ}=54^{\circ}$。
在$\triangle BIC$中,根据三角形内角和为$180^{\circ}$,可得$\angle BIC = 180^{\circ}-(\angle IBC+\angle ICB)=180 - 54 = 126^{\circ}$。
2.当$I$是$\triangle ABC$的外心时:
根据圆周角定理,同弧所对的圆周角是圆心角的一半。
因为$I$是$\triangle ABC$的外心,所以$\angle BIC$是圆心角,$\angle A$是圆周角,且它们所对的弧都是$\overset{\frown}{BC}$,则$\angle BIC = 2\angle A=2×72^{\circ}=144^{\circ}$。
4. 如图,$ \odot O $ 与 $ \triangle ABC $ 各边分别切于点 $ D $、$ E $、$ F $,且 $ \angle C = 60^{\circ} $,$ \angle EOF = 100^{\circ} $. 求 $ \angle B $ 的度数.
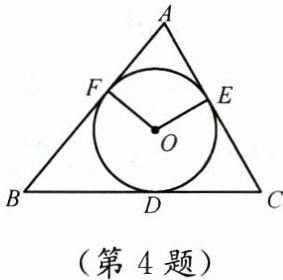

答案:连接OE、OF,
∵⊙O与△ABC各边分别切于点D、E、F,
∴OE⊥AC,OF⊥AB(切线垂直于过切点的半径),
∴∠OEA=∠OFA=90°,
在四边形OFAE中,∠OFA+∠OEA+∠A+∠EOF=360°,
∵∠EOF=100°,
∴∠A=360°-∠OFA-∠OEA-∠EOF=360°-90°-90°-100°=80°,
在△ABC中,∠A+∠B+∠C=180°,∠C=60°,
∴∠B=180°-∠A-∠C=180°-80°-60°=40°.
40°
∵⊙O与△ABC各边分别切于点D、E、F,
∴OE⊥AC,OF⊥AB(切线垂直于过切点的半径),
∴∠OEA=∠OFA=90°,
在四边形OFAE中,∠OFA+∠OEA+∠A+∠EOF=360°,
∵∠EOF=100°,
∴∠A=360°-∠OFA-∠OEA-∠EOF=360°-90°-90°-100°=80°,
在△ABC中,∠A+∠B+∠C=180°,∠C=60°,
∴∠B=180°-∠A-∠C=180°-80°-60°=40°.
40°
1. 如图,$ \triangle ABC $ 的内心为 $ O $,连接 $ AO $ 并延长交 $ \triangle ABC $ 的外接圆于点 $ D $,则线段 $ DO $ 与 $ DB $ 的关系是(

A.$ DO = DB $
B.$ DO > DB $
C.$ DO < DB $
D.不确定
A
)
A.$ DO = DB $
B.$ DO > DB $
C.$ DO < DB $
D.不确定
答案:A
解析:
∵O是△ABC的内心,∴AO平分∠BAC,BO平分∠ABC,即∠BAD=∠CAD,∠ABO=∠CBO。
∵∠CAD=∠CBD(同弧所对的圆周角相等),∴∠BAD=∠CBD。
∵∠DOB=∠BAD+∠ABO(三角形外角性质),∠DBO=∠CBD+∠CBO,
∴∠DOB=∠DBO,∴DB=DO。
∵∠CAD=∠CBD(同弧所对的圆周角相等),∴∠BAD=∠CBD。
∵∠DOB=∠BAD+∠ABO(三角形外角性质),∠DBO=∠CBD+∠CBO,
∴∠DOB=∠DBO,∴DB=DO。
2. 古希腊的几何学家海伦在著作《度量论》中给出了“已知三角形的三边长求三角形面积”的计算公式(海伦公式):$ S = \sqrt{p(p - a)(p - b)(p - c)} $(其中 $ a $、$ b $、$ c $ 是三角形的三边长,$ p = \frac{a + b + c}{2} $,$ S $ 为三角形的面积),并给出了证明. 对于这个问题还可用我国南宋时期数学家秦九韶提出的秦九韶公式解决.
如图,在 $ \triangle ABC $ 中,$ BC = 5 $,$ AC = 6 $,$ AB = 9 $.
(1) 用海伦公式求 $ \triangle ABC $ 的面积;
(2) 求 $ \triangle ABC $ 的内切圆半径 $ r $.

如图,在 $ \triangle ABC $ 中,$ BC = 5 $,$ AC = 6 $,$ AB = 9 $.
(1) 用海伦公式求 $ \triangle ABC $ 的面积;
(2) 求 $ \triangle ABC $ 的内切圆半径 $ r $.

答案:(1)
已知$a = 5$,$b = 6$,$c = 9$,
则$p=\frac{a + b + c}{2}=\frac{5 + 6 + 9}{2}=10$。
$S=\sqrt{p(p - a)(p - b)(p - c)}=\sqrt{10×(10 - 5)×(10 - 6)×(10 - 9)}$
$=\sqrt{10×5×4×1}=\sqrt{200}=10\sqrt{2}$。
(2)
根据三角形面积公式$S = pr$($p$为半周长,$r$为内切圆半径),
已知$S = 10\sqrt{2}$,$p = 10$,
则$r=\frac{S}{p}=\frac{10\sqrt{2}}{10}=\sqrt{2}$。
综上,(1)$\triangle ABC$的面积为$10\sqrt{2}$;(2)$\triangle ABC$的内切圆半径$r$为$\sqrt{2}$。
已知$a = 5$,$b = 6$,$c = 9$,
则$p=\frac{a + b + c}{2}=\frac{5 + 6 + 9}{2}=10$。
$S=\sqrt{p(p - a)(p - b)(p - c)}=\sqrt{10×(10 - 5)×(10 - 6)×(10 - 9)}$
$=\sqrt{10×5×4×1}=\sqrt{200}=10\sqrt{2}$。
(2)
根据三角形面积公式$S = pr$($p$为半周长,$r$为内切圆半径),
已知$S = 10\sqrt{2}$,$p = 10$,
则$r=\frac{S}{p}=\frac{10\sqrt{2}}{10}=\sqrt{2}$。
综上,(1)$\triangle ABC$的面积为$10\sqrt{2}$;(2)$\triangle ABC$的内切圆半径$r$为$\sqrt{2}$。