3. 如图,$ PA $、$ PB $ 分别切 $ \odot O $ 于点 $ A $、$ B $,与 $ \odot O $ 的另一条切线分别相交于点 $ D $、$ C $,若 $ PA = 7 \, cm $,$ \angle P = 45^{\circ} $,则 $ \angle AQB = $
112.5
$ ^{\circ} $,$ \triangle PCD $ 的周长为14cm
.答案:112.5,14cm
解析:
连接OA、OB、OQ,由切线长定理得:DA=DQ,CB=CQ,PA=PB=7cm。△PCD周长=PD+DC+PC=PD+DQ+QC+PC=PD+DA+CB+PC=PA+PB=7+7=14cm。
∵PA、PB是切线,∴OA⊥PA,OB⊥PB,∠OAP=∠OBP=90°。四边形OAPB中,∠AOB=360°-90°-90°-45°=135°。设∠OAQ=∠OQA=α,∠OBQ=∠OQB=β,∠AOQ=180°-2α,∠BOQ=180°-2β,∠AOB=∠AOQ+∠BOQ=360°-2(α+β)=135°,得α+β=112.5°。在△AQB中,∠AQB=180°-(∠QAB+∠QBA)=180°-[(α-22.5°)+(β-22.5°)]=180°-(α+β-45°)=180°-(112.5°-45°)=112.5°。
∵PA、PB是切线,∴OA⊥PA,OB⊥PB,∠OAP=∠OBP=90°。四边形OAPB中,∠AOB=360°-90°-90°-45°=135°。设∠OAQ=∠OQA=α,∠OBQ=∠OQB=β,∠AOQ=180°-2α,∠BOQ=180°-2β,∠AOB=∠AOQ+∠BOQ=360°-2(α+β)=135°,得α+β=112.5°。在△AQB中,∠AQB=180°-(∠QAB+∠QBA)=180°-[(α-22.5°)+(β-22.5°)]=180°-(α+β-45°)=180°-(112.5°-45°)=112.5°。
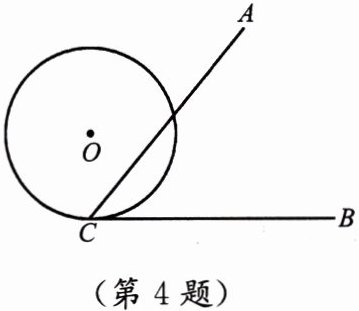
4. 如图,$ \angle ACB = 60^{\circ} $,半径为 $ 1 \, cm $ 的 $ \odot O $ 切 $ BC $ 于点 $ C $,将 $ \odot O $ 沿 $ CB $ 向右滚动,当滚动到 $ \odot O $ 与 $ CA $ 也相切时,圆心 $ O $ 移动的水平距离是
√3
$ cm $.
答案:√3
解析:
初始时,⊙O切BC于C,故OC⊥BC,OC=1cm(半径)。滚动后圆心为O',⊙O'与CA、CB相切,则O'到CA、CB距离均为半径1cm,O'在∠ACB的角平分线上,∠O'CB=30°。在Rt△O'DC中(D为O'在CB上垂足),O'D=1cm,∠O'CD=30°,CD=O'D/tan30°=1/(√3/3)=√3 cm。圆心移动的水平距离即CD=√3 cm。
1. 如图,$ \odot O $ 与正方形 $ ABCD $ 的两边 $ AB $、$ AD $ 相切,且 $ DE $ 与 $ \odot O $ 相切于点 $ E $. 若 $ \odot O $ 的半径为 $ 5 $,且 $ AB = 11 $,则 $ DE = $

6
.
答案:6
解析:
以A为原点,AB为x轴,AD为y轴建立坐标系。则A(0,0),B(11,0),D(0,11),圆心O与AB、AD相切,半径为5,故O(5,5)。D(0,11)在圆外,DE为切线,OE=5(半径),OE⊥DE。OD=√[(5-0)²+(5-11)²]=√61。在Rt△ODE中,DE²=OD²-OE²=61-25=36,DE=6。
2. 如图,在 $ Rt \triangle ABC $ 中,$ \angle C = 90^{\circ} $,$ \odot O $ 内切于 $ \triangle ABC $,切点分别为 $ D $、$ E $、$ F $,则四边形 $ OECF $ 是
正方形
;$ AC = 5 $,$ BC = 12 $,则 $ \odot O $ 的半径是2
.答案:正方形;$2$
解析:
由于$\odot O$是$Rt\triangle ABC$的内切圆,所以$OE\bot AC$,$OF\bot BC$。
因为$\angle C = 90^{\circ}$,所以四边形$OECF$的四个角均为$90^{\circ}$,则四边形$OECF$是矩形。
又因为$OE = OF$(同圆的半径相等),所以矩形$OECF$是正方形。
设$\odot O$的半径为$r$。
根据直角三角形内切圆半径公式$r=\dfrac{a + b-c}{2}$(其中$a$、$b$为直角边,$c$为斜边)。
在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$AC = 5$,$BC = 12$,根据勾股定理$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{5^{2}+12^{2}} = 13$。
把$a = 5$,$b = 12$,$c = 13$代入公式$r=\dfrac{a + b - c}{2}$,可得$r=\dfrac{5 + 12-13}{2}=2$。
因为$\angle C = 90^{\circ}$,所以四边形$OECF$的四个角均为$90^{\circ}$,则四边形$OECF$是矩形。
又因为$OE = OF$(同圆的半径相等),所以矩形$OECF$是正方形。
设$\odot O$的半径为$r$。
根据直角三角形内切圆半径公式$r=\dfrac{a + b-c}{2}$(其中$a$、$b$为直角边,$c$为斜边)。
在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$AC = 5$,$BC = 12$,根据勾股定理$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{5^{2}+12^{2}} = 13$。
把$a = 5$,$b = 12$,$c = 13$代入公式$r=\dfrac{a + b - c}{2}$,可得$r=\dfrac{5 + 12-13}{2}=2$。
3. 如图,在 $ Rt \triangle ABC $ 中,$ \angle ACB = 90^{\circ} $,以 $ AC $ 为直径的 $ \odot O $ 与边 $ AB $ 交于点 $ D $,过点 $ D $ 的切线 $ DE $ 交 $ BC $ 于点 $ E $.
(1)求证:$ EB = EC $;
(2)若以 $ O $、$ D $、$ E $、$ C $ 为顶点的四边形是矩形,试判断 $ \triangle ABC $ 的形状,并说明理由.

(1)求证:$ EB = EC $;
(2)若以 $ O $、$ D $、$ E $、$ C $ 为顶点的四边形是矩形,试判断 $ \triangle ABC $ 的形状,并说明理由.

答案:(1)连接OD、CD.
∵AC是⊙O直径,∴∠ADC=90°.
∵DE是⊙O切线,∴OD⊥DE,∠ODE=90°.
在Rt△ODE和Rt△OCE中,OD=OC,OE=OE,
∴Rt△ODE≌Rt△OCE(HL),∴DE=CE.
∴∠EDC=∠ECD.
∵∠ACB=90°,∠ADC=90°,
∴∠B+∠ECD=90°,∠EDC+∠EDB=90°.
∴∠EDB=∠B,∴EB=ED.
∴EB=EC.
(2)△ABC是等腰直角三角形.
理由:∵四边形ODEC是矩形,∴OD=EC.
∵OD=OC=AC/2,∴EC=AC/2.
由(1)知EB=EC,∴BC=2EC=AC.
∵∠ACB=90°,∴△ABC是等腰直角三角形.
∵AC是⊙O直径,∴∠ADC=90°.
∵DE是⊙O切线,∴OD⊥DE,∠ODE=90°.
在Rt△ODE和Rt△OCE中,OD=OC,OE=OE,
∴Rt△ODE≌Rt△OCE(HL),∴DE=CE.
∴∠EDC=∠ECD.
∵∠ACB=90°,∠ADC=90°,
∴∠B+∠ECD=90°,∠EDC+∠EDB=90°.
∴∠EDB=∠B,∴EB=ED.
∴EB=EC.
(2)△ABC是等腰直角三角形.
理由:∵四边形ODEC是矩形,∴OD=EC.
∵OD=OC=AC/2,∴EC=AC/2.
由(1)知EB=EC,∴BC=2EC=AC.
∵∠ACB=90°,∴△ABC是等腰直角三角形.