1. 把一个圆四等分,再顺次连接各等分点,判断所得图形的形状,它与该圆有什么关系?
答案:将一个圆四等分,则每段弧所对的圆心角为 $360^{\circ} ÷ 4 = 90^{\circ}$。
顺次连接各等分点,由于每段弧的度数相等,所以各边相等(在同圆或等圆中,相等的圆心角所对的弦相等)。
同时,由于圆心角为 $90^{\circ}$,根据圆周角定理的推论(或直观判断),所得的四边形每个角都是 $90^{\circ}$。
因此,所得图形是正方形。
该正方形内接于该圆。
顺次连接各等分点,由于每段弧的度数相等,所以各边相等(在同圆或等圆中,相等的圆心角所对的弦相等)。
同时,由于圆心角为 $90^{\circ}$,根据圆周角定理的推论(或直观判断),所得的四边形每个角都是 $90^{\circ}$。
因此,所得图形是正方形。
该正方形内接于该圆。
2. 把一个圆五等分后,顺次连接各等分点,所得图形的形状又如何?
一般地,要把一个圆 $ n $ 等分,只要把圆的周角 $ n $ 等分即可,每一个圆心角的度数是
正五边形
一般地,要把一个圆 $ n $ 等分,只要把圆的周角 $ n $ 等分即可,每一个圆心角的度数是
$\frac{360^\circ}{n}$
.答案:正五边形;$\frac{360^\circ}{n}$
3. 在正多边形的定义中,能不能省去“各角相等”或“各边相等”? 请举例说明.
答案:不能省去“各角相等”或“各边相等”。
若省去“各角相等”,仅“各边相等”:如菱形,四边相等,但各角不一定相等(邻角互补,非直角时不都相等),不是正多边形。
若省去“各边相等”,仅“各角相等”:如矩形,四角相等(均为直角),但各边不一定相等(长≠宽时),不是正多边形。
若省去“各角相等”,仅“各边相等”:如菱形,四边相等,但各角不一定相等(邻角互补,非直角时不都相等),不是正多边形。
若省去“各边相等”,仅“各角相等”:如矩形,四角相等(均为直角),但各边不一定相等(长≠宽时),不是正多边形。
1. 探索正多边形的半径和边长之间的关系
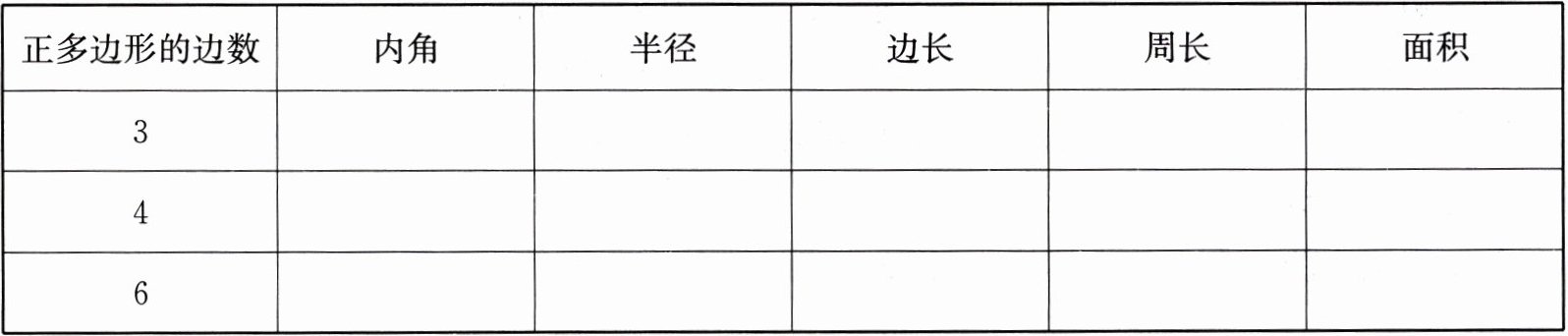

答案:|正多边形的边数|内角|半径|边长|周长|面积|
|----|----|----|----|----|----|
|3|60°|R|√3R|3√3R|(3√3/4)R²|
|4|90°|R|√2R|4√2R|2R²|
|6|120°|R|R|6R|(3√3/2)R²|
|----|----|----|----|----|----|
|3|60°|R|√3R|3√3R|(3√3/4)R²|
|4|90°|R|√2R|4√2R|2R²|
|6|120°|R|R|6R|(3√3/2)R²|
2. 如图 $ 2 - 22 $,正三角形纸片 $ ABC $ 的边长为6,如何剪去3个三角形从而得到一个正六边形纸片 $ DEG KHF $? 你能求出这个正六边形的面积吗?


答案:1. 在正三角形ABC的每条边上,分别取距离两端顶点均为2的两点,连接这六个点,剪去三个顶点处的小正三角形(边长为2),即可得到正六边形DEG KHF。
2. 正六边形面积计算:
原正三角形ABC面积:$ S_{\triangle ABC} = \frac{\sqrt{3}}{4} × 6^2 = 9\sqrt{3} $
每个小正三角形面积:$ S_{小} = \frac{\sqrt{3}}{4} × 2^2 = \sqrt{3} $
三个小正三角形总面积:$ 3S_{小} = 3\sqrt{3} $
正六边形面积:$ S = 9\sqrt{3} - 3\sqrt{3} = 6\sqrt{3} $
结论:剪去三个边长为2的小正三角形;正六边形面积为$ 6\sqrt{3} $。
2. 正六边形面积计算:
原正三角形ABC面积:$ S_{\triangle ABC} = \frac{\sqrt{3}}{4} × 6^2 = 9\sqrt{3} $
每个小正三角形面积:$ S_{小} = \frac{\sqrt{3}}{4} × 2^2 = \sqrt{3} $
三个小正三角形总面积:$ 3S_{小} = 3\sqrt{3} $
正六边形面积:$ S = 9\sqrt{3} - 3\sqrt{3} = 6\sqrt{3} $
结论:剪去三个边长为2的小正三角形;正六边形面积为$ 6\sqrt{3} $。