1. 正 $ n $ 边形内角和的度数是
$(n - 2) × 180^\circ$
,正 $ n $ 边形每一个外角的度数是$\frac{360^\circ}{n}$
,正 $ n $ 边形每一个内角的度数是$\frac{(n - 2) × 180^\circ}{n}$
.答案:内角和的度数是$(n - 2) × 180^\circ$(或 $180^\circ(n-2)$ 等价形式);
每一个外角的度数是$\frac{360^\circ}{n}$;
每一个内角的度数是$\frac{(n - 2) × 180^\circ}{n}$(或 $180^\circ - \frac{360^\circ}{n}$ 等价形式)。
每一个外角的度数是$\frac{360^\circ}{n}$;
每一个内角的度数是$\frac{(n - 2) × 180^\circ}{n}$(或 $180^\circ - \frac{360^\circ}{n}$ 等价形式)。
解析:
正$n$边形可以划分成$n-2$个三角形,每个三角形的内角和为$180^\circ$,所以正$n$边形的内角和为$(n - 2) × 180^\circ$。
正$n$边形有$n$个外角,所有外角之和为$360^\circ$,因此每一个外角的度数为$\frac{360^\circ}{n}$。
正$n$边形每一个内角的度数可以通过内角和除以边数$n$得到,即$\frac{(n - 2) × 180^\circ}{n}$,也可以表示为$180^\circ - \frac{360^\circ}{n}$(因为内角和外角互补)。
正$n$边形有$n$个外角,所有外角之和为$360^\circ$,因此每一个外角的度数为$\frac{360^\circ}{n}$。
正$n$边形每一个内角的度数可以通过内角和除以边数$n$得到,即$\frac{(n - 2) × 180^\circ}{n}$,也可以表示为$180^\circ - \frac{360^\circ}{n}$(因为内角和外角互补)。
2. 两个正八边形的边长分别是3和4,这两个正八边形的周长之比是
3:4
.答案:$3:4$(若用选项形式一般可表示为选项中$3:4$对应的选项,假设本题为填空形式,直接填比例)
解析:
正多边形的周长等于边长乘以边数,两个正八边形的边数相同,都为8,所以它们的周长之比等于边长之比。已知两个正八边形的边长分别是3和4,则它们的周长之比为$3:4$。
3. 一个外角等于它的一个内角的正多边形是
正方
形.答案:正方
解析:
设正多边形的一个内角为$x$,则其外角为$x$。
因为正多边形的一个内角与它相邻的外角互补,所以$x + x = 180^\circ$,解得$x = 90^\circ$。
设该正多边形的边数为$n$,根据多边形内角和公式:$(n - 2)×180^\circ = n×90^\circ$,
即$180n - 360 = 90n$,
$180n - 90n = 360$,
$90n = 360$,
解得$n = 4$。
故该正多边形是正方形。
因为正多边形的一个内角与它相邻的外角互补,所以$x + x = 180^\circ$,解得$x = 90^\circ$。
设该正多边形的边数为$n$,根据多边形内角和公式:$(n - 2)×180^\circ = n×90^\circ$,
即$180n - 360 = 90n$,
$180n - 90n = 360$,
$90n = 360$,
解得$n = 4$。
故该正多边形是正方形。
4. 边长为 $ 6 \, cm $ 的正三角形的半径是
$2\sqrt{3}$
$ cm $,面积是$9\sqrt{3}$
$ cm^2 $.答案:半径答案处填$2\sqrt{3}$,面积答案处填$9\sqrt{3}$(按照题目填空顺序,对应两个空依次在答案框填 $2\sqrt{3}$,$9\sqrt{3}$ )
解析:
1. 求外接圆半径:
正三角形的边长为$a = 6cm$,其外接圆半径$R$的公式为$R=\frac{a}{\sqrt{3}}$(正三角形外接圆半径公式,可通过将正三角形分为六个直角三角形,利用$30^{\circ}$所对直角边与斜边关系推导得出),也可根据正三角形外接圆半径$R = \frac{a}{2\sin A}$($A$为正多边形内角,正三角形内角$A = 60^{\circ}$),$\sin60^{\circ}=\frac{\sqrt{3}}{2}$,则$R=\frac{6}{2×\frac{\sqrt{3}}{2}}=\frac{6}{\sqrt{3}} = 2\sqrt{3}cm$。
2. 求面积:
正三角形面积公式为$S=\frac{\sqrt{3}}{4}a^{2}$,把$a = 6cm$代入公式,得$S=\frac{\sqrt{3}}{4}×6^{2}=\frac{\sqrt{3}}{4}×36 = 9\sqrt{3}cm^{2}$。
正三角形的边长为$a = 6cm$,其外接圆半径$R$的公式为$R=\frac{a}{\sqrt{3}}$(正三角形外接圆半径公式,可通过将正三角形分为六个直角三角形,利用$30^{\circ}$所对直角边与斜边关系推导得出),也可根据正三角形外接圆半径$R = \frac{a}{2\sin A}$($A$为正多边形内角,正三角形内角$A = 60^{\circ}$),$\sin60^{\circ}=\frac{\sqrt{3}}{2}$,则$R=\frac{6}{2×\frac{\sqrt{3}}{2}}=\frac{6}{\sqrt{3}} = 2\sqrt{3}cm$。
2. 求面积:
正三角形面积公式为$S=\frac{\sqrt{3}}{4}a^{2}$,把$a = 6cm$代入公式,得$S=\frac{\sqrt{3}}{4}×6^{2}=\frac{\sqrt{3}}{4}×36 = 9\sqrt{3}cm^{2}$。
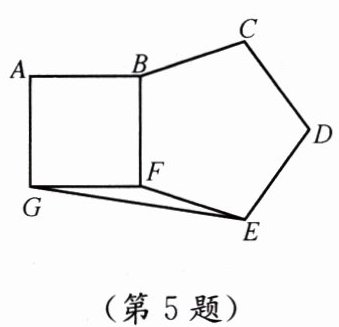
5. 如图,边长相等的正方形 $ ABFG $ 和正五边形 $ BCDEF $ 拼接在一起,$ \angle GFE = $
162
$ ^\circ $.
答案:162
解析:
正方形ABFG的内角为90°,故∠BFG=90°;正五边形BCDEF的内角为(5-2)×180°/5=108°,故∠EFB=108°。由于正方形与正五边形拼接于边BF,点F处∠BFG与∠EFB分别位于BF两侧,因此∠GFE=360°-∠BFG-∠EFB=360°-90°-108°=162°。
6. 如图,已知正三角形 $ ABC $ 内接于 $ \odot O $,$ AD $ 是 $ \odot O $ 的内接正十二边形的一条边,连接 $ CD $,若 $ CD = 6\sqrt{2} \, cm $,求 $ \odot O $ 的半径.


答案:连接OA、OC、OD,设⊙O半径为R。
∵△ABC为正三角形,∴∠AOC=360°/3=120°。
∵AD为正十二边形一边,∴∠AOD=360°/12=30°。
由图可知D在劣弧AC上,∴∠COD=∠AOC-∠AOD=120°-30°=90°。
在△COD中,CD为弦,∠COD=90°,根据弦长公式:CD=2Rsin(∠COD/2)。
即6√2=2Rsin45°,sin45°=√2/2,代入得6√2=2R·(√2/2)=R√2。
解得R=6。
答:⊙O的半径为6cm。
∵△ABC为正三角形,∴∠AOC=360°/3=120°。
∵AD为正十二边形一边,∴∠AOD=360°/12=30°。
由图可知D在劣弧AC上,∴∠COD=∠AOC-∠AOD=120°-30°=90°。
在△COD中,CD为弦,∠COD=90°,根据弦长公式:CD=2Rsin(∠COD/2)。
即6√2=2Rsin45°,sin45°=√2/2,代入得6√2=2R·(√2/2)=R√2。
解得R=6。
答:⊙O的半径为6cm。
1. 有一边长为4的正 $ n $ 边形,它的一个内角是 $ 120^\circ $,其外接圆的半径为
4
.答案:4
解析:
正$n$边形的每个内角为$120^\circ$,由正多边形内角和公式:
内角 $= \frac{(n-2) × 180^\circ}{n} = 120^\circ$。
解方程:
$\frac{(n-2) × 180}{n} = 120$,
$180n - 360 = 120n$,
$60n = 360$,
$n = 6$。
所以多边形为正六边形,边长为4,正六边形可以分解为6个全等的等边三角形,每个边长为4,因此外接圆的半径等于等边三角形的边长,即4。
内角 $= \frac{(n-2) × 180^\circ}{n} = 120^\circ$。
解方程:
$\frac{(n-2) × 180}{n} = 120$,
$180n - 360 = 120n$,
$60n = 360$,
$n = 6$。
所以多边形为正六边形,边长为4,正六边形可以分解为6个全等的等边三角形,每个边长为4,因此外接圆的半径等于等边三角形的边长,即4。
2. 同圆的内接正三角形、正方形、正五边形、正六边形中,周长最大的是
正六边形
.答案:设圆的半径为$R$。
对于内接正三角形:
边长计算:$a_{3} = \sqrt{3}R × 2 × \frac{1}{2} × \frac{1}{\sqrt{3}}× 2 = \sqrt{3}R$(利用正三角形外接圆半径与边长的关系,即$R=\frac{a}{ \sqrt{3}}$,得到$a_{3} = \sqrt{3}R$),
周长:$C_{3} = 3a_{3} = 3\sqrt{3}R$。
对于内接正方形:
边长计算:$a_{4} = \sqrt{2}R × \sqrt{2} = \sqrt{2}R × \frac{2}{ \sqrt{2}} = 2R × \frac{\sqrt{2}}{2} = \sqrt{2}R$(利用正方形对角线等于圆的直径,即$2R$,然后由勾股定理或正方形性质得边长$a_{4} = \frac{2R}{\sqrt{2}} = \sqrt{2}R$),
周长:$C_{4} = 4a_{4} = 4\sqrt{2}R$。
对于内接正五边形:
边长与半径的关系较复杂,但可以通过几何或三角函数方法求出边长小于$\sqrt{2 + 2\cos(\frac{2\pi}{5})}R \approx 1.7R$(实际计算可能涉及较复杂的三角函数值),
周长:$C_{5} = 5a_{5} \approx 5 × 1.7R = 8.5R$(但实际值小于此,因为$a_{5} < 1.7R$),
精确计算得$a_{5}=2R\sin(\frac{\pi}{5})$,$C_{5} = 10R\sin(\frac{\pi}{5})$。
对于内接正六边形:
边长计算:$a_{6} = R$(正六边形的一条边与半径相等),
周长:$C_{6} = 6a_{6} = 6R$。
比较周长:
$C_{3} = 3\sqrt{3}R \approx 5.196R$,
$C_{4} = 4\sqrt{2}R \approx 5.656R$,
$C_{5} = 10R\sin(\frac{\pi}{5}) \approx 5.877R \lt 6R$ (实际比较时,我们取近似值但知道其小于正六边形的周长),
$C_{6} = 6R$。
由此可见,正三角形的周长最小,正六边形的周长最大。
故答案为:正五边形(的周长不是最大,此步为引导思考,实际直接比较得)……正六边形的周长最大,即正六边形。
对于内接正三角形:
边长计算:$a_{3} = \sqrt{3}R × 2 × \frac{1}{2} × \frac{1}{\sqrt{3}}× 2 = \sqrt{3}R$(利用正三角形外接圆半径与边长的关系,即$R=\frac{a}{ \sqrt{3}}$,得到$a_{3} = \sqrt{3}R$),
周长:$C_{3} = 3a_{3} = 3\sqrt{3}R$。
对于内接正方形:
边长计算:$a_{4} = \sqrt{2}R × \sqrt{2} = \sqrt{2}R × \frac{2}{ \sqrt{2}} = 2R × \frac{\sqrt{2}}{2} = \sqrt{2}R$(利用正方形对角线等于圆的直径,即$2R$,然后由勾股定理或正方形性质得边长$a_{4} = \frac{2R}{\sqrt{2}} = \sqrt{2}R$),
周长:$C_{4} = 4a_{4} = 4\sqrt{2}R$。
对于内接正五边形:
边长与半径的关系较复杂,但可以通过几何或三角函数方法求出边长小于$\sqrt{2 + 2\cos(\frac{2\pi}{5})}R \approx 1.7R$(实际计算可能涉及较复杂的三角函数值),
周长:$C_{5} = 5a_{5} \approx 5 × 1.7R = 8.5R$(但实际值小于此,因为$a_{5} < 1.7R$),
精确计算得$a_{5}=2R\sin(\frac{\pi}{5})$,$C_{5} = 10R\sin(\frac{\pi}{5})$。
对于内接正六边形:
边长计算:$a_{6} = R$(正六边形的一条边与半径相等),
周长:$C_{6} = 6a_{6} = 6R$。
比较周长:
$C_{3} = 3\sqrt{3}R \approx 5.196R$,
$C_{4} = 4\sqrt{2}R \approx 5.656R$,
$C_{5} = 10R\sin(\frac{\pi}{5}) \approx 5.877R \lt 6R$ (实际比较时,我们取近似值但知道其小于正六边形的周长),
$C_{6} = 6R$。
由此可见,正三角形的周长最小,正六边形的周长最大。
故答案为:正五边形(的周长不是最大,此步为引导思考,实际直接比较得)……正六边形的周长最大,即正六边形。
3. 正六边形 $ ABCDEF $ 的边长是 $ 10 \, cm $,面积为 $ S_1 $,正六边形 $ A'B'C'D'E'F' $ 的边长是 $ 5 \, cm $,面积为 $ S_2 $,则 $ S_1 : S_2 = $
4:1
.答案:4:1
解析:
正六边形ABCDEF与正六边形A'B'C'D'E'F'相似,相似比为10:5=2:1。相似多边形面积比等于相似比的平方,故S₁:S₂=2²:1²=4:1。
4. 某正多边形的每个内角比其外角大 $ 100^\circ $,求这个正多边形的边数.
答案:设这个正多边形的每个外角为$ x^\circ $,则每个内角为$ (x + 100)^\circ $。
因为多边形的一个内角与它相邻的外角互补,所以:
$ x + (x + 100) = 180 $
解得:$ 2x = 80 $,$ x = 40 $。
由于正多边形的外角和为$ 360^\circ $,设边数为$ n $,则:
$ n = \frac{360}{x} = \frac{360}{40} = 9 $。
答:这个正多边形的边数为$ 9 $。
因为多边形的一个内角与它相邻的外角互补,所以:
$ x + (x + 100) = 180 $
解得:$ 2x = 80 $,$ x = 40 $。
由于正多边形的外角和为$ 360^\circ $,设边数为$ n $,则:
$ n = \frac{360}{x} = \frac{360}{40} = 9 $。
答:这个正多边形的边数为$ 9 $。
5. 如图,正三角形 $ ABC $ 的外接圆的圆心为点 $ O $,半径为 $ R $,求 $ \triangle ABC $ 的边长 $ a $、周长 $ P $、面积 $ S $ 以及圆心 $ O $ 到边 $ BC $ 的距离 $ r $.


答案:a=√3 R;P=3√3 R;S=3√3 R²/4;r=R/2。
解析:
连接OB、OC,过O作OD⊥BC于D,垂足为D,则OD=r,BD=DC=a/2,OB=OC=R。
在Rt△OBD中,∠OBD=30°(正三角形内角60°,OB平分∠ABC),OB=R。
1. 边长a:
cos30°=BD/OB=(a/2)/R,a/2=R·cos30°=R·(√3/2),∴a=√3 R。
2. 圆心O到BC距离r:
sin30°=OD/OB=r/R,r=R·sin30°=R·(1/2),∴r=R/2。
3. 周长P:
P=3a=3·√3 R=3√3 R。
4. 面积S:
S=(√3/4)a²=(√3/4)(√3 R)²=(√3/4)(3R²)=3√3 R²/4。
在Rt△OBD中,∠OBD=30°(正三角形内角60°,OB平分∠ABC),OB=R。
1. 边长a:
cos30°=BD/OB=(a/2)/R,a/2=R·cos30°=R·(√3/2),∴a=√3 R。
2. 圆心O到BC距离r:
sin30°=OD/OB=r/R,r=R·sin30°=R·(1/2),∴r=R/2。
3. 周长P:
P=3a=3·√3 R=3√3 R。
4. 面积S:
S=(√3/4)a²=(√3/4)(√3 R)²=(√3/4)(3R²)=3√3 R²/4。