2. 一个正多边形绕它的中心旋转 $60^{\circ}$ 和原来的图形重合, 这个正多边形可能是 ______
正六边形(或正三角形)
.答案:正六边形(或正三角形)
解析:
正多边形绕中心旋转重合的最小角度为$\frac{360^{\circ}}{n}$($n$为边数,$n\geq3$且为整数)。已知旋转$60^{\circ}$重合,则$\frac{360^{\circ}}{n}$为$60^{\circ}$的约数,即$n=\frac{360^{\circ}}{k\cdot60^{\circ}}=\frac{6}{k}$($k$为正整数)。当$k=1$时,$n=6$;当$k=2$时,$n=3$;当$k=3$时,$n=2$(舍去)。故可能是正三角形或正六边形。
3. 正方形
是
正多边形, 正三角形 ______ 是
正多边形, 菱形 ______ 不是
正多边形. (填“是”或“不是”)答案:是,是,不是
解析:
根据正多边形的定义,正多边形是各边相等,各角也相等的多边形。
正方形四边相等,四个角均为$90^\circ$,满足正多边形的定义,所以正方形是正多边形。
正三角形三条边相等,三个角均为$60^\circ$,满足正多边形的定义,所以正三角形是正多边形。
菱形虽然四边相等,但其角不一定相等,不满足正多边形各角也相等的条件,所以菱形不是正多边形。
正方形四边相等,四个角均为$90^\circ$,满足正多边形的定义,所以正方形是正多边形。
正三角形三条边相等,三个角均为$60^\circ$,满足正多边形的定义,所以正三角形是正多边形。
菱形虽然四边相等,但其角不一定相等,不满足正多边形各角也相等的条件,所以菱形不是正多边形。
4. 如图, $\odot O$ 是正方形 $ABCD$ 与正六边形 $AEFCGH$ 的外接圆.
(1) 正方形 $ABCD$ 与正六边形 $AEFCGH$ 的边长之比为 ______
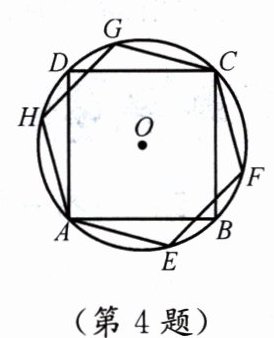
(1) 正方形 $ABCD$ 与正六边形 $AEFCGH$ 的边长之比为 ______
$\sqrt{2}:1$
.是,$n=12$

答案:(1) 设$\odot O$的半径为$R$。
正六边形$AEFCGH$的边长等于外接圆半径,故其边长$a_6=R$。
正方形$ABCD$的对角线为外接圆直径$2R$,设边长为$a_4$,由勾股定理得$a_4^2+a_4^2=(2R)^2$,解得$a_4=\sqrt{2}R$。
则正方形与正六边形边长之比为$\sqrt{2}R:R=\sqrt{2}:1$。
(2) 连接$OA,OB,OE$。
正六边形中心角为$\frac{360^\circ}{6}=60^\circ$,故$\angle AOE=60^\circ$。
正方形中心角为$\frac{360^\circ}{4}=90^\circ$,故$\angle AOB=90^\circ$。
$\angle BOE=\angle AOB-\angle AOE=90^\circ-60^\circ=30^\circ$。
$\because\frac{360^\circ}{30^\circ}=12$,$\therefore BE$是$\odot O$内接正十二边形的一边,$n=12$。
(1)$\sqrt{2}:1$
(2)是,$n=12$
正六边形$AEFCGH$的边长等于外接圆半径,故其边长$a_6=R$。
正方形$ABCD$的对角线为外接圆直径$2R$,设边长为$a_4$,由勾股定理得$a_4^2+a_4^2=(2R)^2$,解得$a_4=\sqrt{2}R$。
则正方形与正六边形边长之比为$\sqrt{2}R:R=\sqrt{2}:1$。
(2) 连接$OA,OB,OE$。
正六边形中心角为$\frac{360^\circ}{6}=60^\circ$,故$\angle AOE=60^\circ$。
正方形中心角为$\frac{360^\circ}{4}=90^\circ$,故$\angle AOB=90^\circ$。
$\angle BOE=\angle AOB-\angle AOE=90^\circ-60^\circ=30^\circ$。
$\because\frac{360^\circ}{30^\circ}=12$,$\therefore BE$是$\odot O$内接正十二边形的一边,$n=12$。
(1)$\sqrt{2}:1$
(2)是,$n=12$
1. 已知一个边长为 $3\mathrm{cm}$ 的正方形, 若要剪一张圆形纸片完全盖住这个正方形, 则这个圆形纸片的半径最小为
$\frac{3\sqrt{2}}{2}$
.答案:$\frac{3\sqrt{2}}{2}cm$(或写为$\frac{3}{2}\sqrt{2}cm$,根据题目要求填半径最小值对应的答案形式,若为填空题则直接填数值)由于这里是填空(根据问题描述),直接给数值形式:$\frac{3\sqrt{2}}{2}$(若需要简化成小数等,根据题目具体要求,这里保持根式)
解析:
要使圆形纸片完全盖住边长为$3cm$的正方形,则圆形为正方形的外接圆,其直径应等于正方形的对角线长度。
由勾股定理,正方形的对角线长为:
$\sqrt{3^2 + 3^2} = \sqrt{18} = 3\sqrt{2} (cm)$
因此,圆形纸片的最小半径为对角线的一半:
$\frac{3\sqrt{2}}{2} cm$
由勾股定理,正方形的对角线长为:
$\sqrt{3^2 + 3^2} = \sqrt{18} = 3\sqrt{2} (cm)$
因此,圆形纸片的最小半径为对角线的一半:
$\frac{3\sqrt{2}}{2} cm$
2. 把边长为 $12$ 的等边三角形纸板剪去三个全等的小等边三角形, 得到一个正六边形, 则这个正六边形的边长是 (
A.$6$
B.$4$
C.$8$
D.$9$
B
)A.$6$
B.$4$
C.$8$
D.$9$
答案:B
解析:
设正六边形的边长为 $ x $。由于剪去的三个小等边三角形全等,其边长也为 $ x $。原等边三角形边长为12,每条边上被剪去两个小三角形的边和中间正六边形的边,即 $ x + x + x = 12 $,解得 $ x = 4 $。
3. 周长相等的正方形与正六边形的面积分别为 $S_1$、$S_2$, $S_1$ 和 $S_2$ 的关系为 (
A.$S_1 < S_2$
B.$S_1 = S_2$
C.$S_1 > S_2$
D.无法确定
A
)A.$S_1 < S_2$
B.$S_1 = S_2$
C.$S_1 > S_2$
D.无法确定
答案:A
解析:
设正方形和正六边形的周长为$l$。
正方形的边长为$\frac{l}{4}$,其面积$S_1 = \left( \frac{l}{4} \right)^2 = \frac{l^2}{16}$。
正六边形边长为$\frac{l}{6}$,可分割为6个等边三角形,每个三角形面积为$\frac{\sqrt{3}}{4} \left( \frac{l}{6} \right)^2$,总面积$S_2 = 6 × \frac{\sqrt{3}}{4} \left( \frac{l}{6} \right)^2 = \frac{\sqrt{3} l^2}{24}$。
比较$\frac{S_1}{S_2} = \frac{\frac{l^2}{16}}{\frac{\sqrt{3} l^2}{24}} = \frac{24}{16\sqrt{3}} = \frac{\sqrt{3}}{2} < 1$,故$S_1 < S_2$。
正方形的边长为$\frac{l}{4}$,其面积$S_1 = \left( \frac{l}{4} \right)^2 = \frac{l^2}{16}$。
正六边形边长为$\frac{l}{6}$,可分割为6个等边三角形,每个三角形面积为$\frac{\sqrt{3}}{4} \left( \frac{l}{6} \right)^2$,总面积$S_2 = 6 × \frac{\sqrt{3}}{4} \left( \frac{l}{6} \right)^2 = \frac{\sqrt{3} l^2}{24}$。
比较$\frac{S_1}{S_2} = \frac{\frac{l^2}{16}}{\frac{\sqrt{3} l^2}{24}} = \frac{24}{16\sqrt{3}} = \frac{\sqrt{3}}{2} < 1$,故$S_1 < S_2$。
4. 如图, $\triangle ABC$ 是 $\odot O$ 的内接正三角形, 四边形 $DEFG$ 是 $\odot O$ 的内接正方形, $EF // BC$. 由此可知 $\angle AOF$ 为 (

A.$125^{\circ}$
B.$130^{\circ}$
C.$135^{\circ}$
D.$140^{\circ}$
C
)
A.$125^{\circ}$
B.$130^{\circ}$
C.$135^{\circ}$
D.$140^{\circ}$
答案:C
解析:
连接$OA$,$OC$,$OC$与$EF$交点为$H$。
$\triangle ABC$是$\odot O$内接正三角形,
$\therefore \angle AOC = 120^{\circ}$。
四边形$DEFG$是$\odot O$的内接正方形,
$\therefore \angle EOF = 90^{\circ}$,$OH\bot EF$。
$\because EF// BC$,
$\therefore OH\bot BC$,
$\therefore$点$H$是$BC$中点,
$\therefore \angle AOH = \frac{1}{2}\angle AOC = 60^{\circ}$,
$\therefore \angle AOF = \angle AOH + \angle HOF = 60^{\circ}+ 45^{\circ}= 135^{\circ}$。
$\triangle ABC$是$\odot O$内接正三角形,
$\therefore \angle AOC = 120^{\circ}$。
四边形$DEFG$是$\odot O$的内接正方形,
$\therefore \angle EOF = 90^{\circ}$,$OH\bot EF$。
$\because EF// BC$,
$\therefore OH\bot BC$,
$\therefore$点$H$是$BC$中点,
$\therefore \angle AOH = \frac{1}{2}\angle AOC = 60^{\circ}$,
$\therefore \angle AOF = \angle AOH + \angle HOF = 60^{\circ}+ 45^{\circ}= 135^{\circ}$。
5. 如图, $EF$ 是 $\odot O$ 的直径.
(1) 请用直尺和圆规作出 $\odot O$ 的内接正方形 $ABCD$, 要求所作正方形的一组对边 $AD$、$BC$ 分别垂直于 $EF$; (不写作法, 保留作图痕迹)
(2) 在所作的图中, 连接 $EA$、$EB$, 求出 $\angle EAD$、$\angle EBC$ 的度数.

(1) 请用直尺和圆规作出 $\odot O$ 的内接正方形 $ABCD$, 要求所作正方形的一组对边 $AD$、$BC$ 分别垂直于 $EF$; (不写作法, 保留作图痕迹)
(2) 在所作的图中, 连接 $EA$、$EB$, 求出 $\angle EAD$、$\angle EBC$ 的度数.

答案:(1) 作图痕迹:以EF为直径,过圆心O作EF的垂直平分线,交圆于两点,再分别过EF上距O点等距的两点作EF的垂线,交圆于A、D和B、C,顺次连接A、B、C、D(保留作图痕迹)。
(2) ∠EAD=22.5°,∠EBC=67.5°。
(2) ∠EAD=22.5°,∠EBC=67.5°。
解析:
(1) 作图痕迹如图所示(此处需实际作图,以EF为直径作圆,作EF的垂直平分线交圆于A、C两点,连接A、B、C、D得正方形ABCD,其中AD、BC垂直于EF)。
(2) 连接OA、OB。
因为四边形ABCD是⊙O的内接正方形,所以∠AOB=90°,OA=OB。
又因为EF是直径,AD⊥EF,所以∠AOE=45°。
在△AOE中,OA=OE,所以∠OAE=∠OEA=(180°-45°)/2=67.5°。
因为AD⊥EF,所以∠OAD=45°,则∠EAD=∠OAE - ∠OAD=67.5° - 45°=22.5°。
同理,∠EBC=22.5°。
∠EAD=22.5°,∠EBC=22.5°