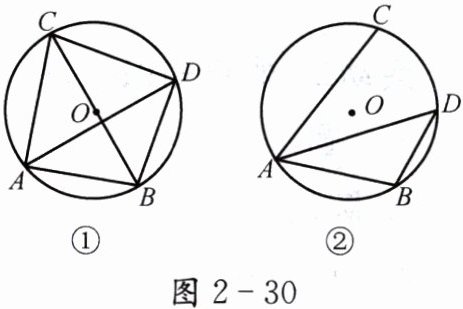
如图$2 - 30$,已知$\odot O的直径为10$,点$A$、$B$、$C在\odot O$上,$\angle CAB的平分线交\odot O于点D$.
(1) 如图①,若$\angle BDC = 90^{\circ}$,$AB = 6$,求$AC$、$BD$、$CD$的长;
(2) 如图②,若$\angle CAB = 60^{\circ}$,求$BD$的长.
(1) 如图①,若$\angle BDC = 90^{\circ}$,$AB = 6$,求$AC$、$BD$、$CD$的长;
(2) 如图②,若$\angle CAB = 60^{\circ}$,求$BD$的长.

答案:(1)
1. 求$AC$的长:
因为$\angle BDC = 90^{\circ}$,所以$\angle BAC=90^{\circ}$(同弧所对的圆周角相等,$\angle BDC$与$\angle BAC$所对的弧都是$\overset{\frown}{BC}$)。
已知$AB = 6$,$\odot O$的直径为$10$,则$BC$为直径$=10$。
在$Rt\triangle ABC$中,根据勾股定理$AC=\sqrt{BC^{2}-AB^{2}}=\sqrt{10^{2}-6^{2}} = 8$。
2. 求$BD$、$CD$的长:
因为$AD$平分$\angle CAB$,所以$\angle CAD=\angle BAD$,则$CD = BD$。
在$Rt\triangle BCD$中,$BC = 10$,根据勾股定理$BD^{2}+CD^{2}=BC^{2}$,又$CD = BD$,所以$2BD^{2}=100$,解得$BD = CD = 5\sqrt{2}$。
(2)
连接$OB$、$OD$,因为$AD$平分$\angle CAB$,$\angle CAB = 60^{\circ}$,所以$\angle DAB=\frac{1}{2}\angle CAB = 30^{\circ}$。
根据同弧所对的圆心角是圆周角的$2$倍,$\angle BOD = 2\angle BAD=60^{\circ}$。
又因为$OB = OD$,所以$\triangle BOD$是等边三角形。
已知$\odot O$的直径为$10$,则半径$OB = 5$,所以$BD = OB = 5$。
综上,(1)中$AC = 8$,$BD = 5\sqrt{2}$,$CD = 5\sqrt{2}$;(2)中$BD$的长为$5$。
1. 求$AC$的长:
因为$\angle BDC = 90^{\circ}$,所以$\angle BAC=90^{\circ}$(同弧所对的圆周角相等,$\angle BDC$与$\angle BAC$所对的弧都是$\overset{\frown}{BC}$)。
已知$AB = 6$,$\odot O$的直径为$10$,则$BC$为直径$=10$。
在$Rt\triangle ABC$中,根据勾股定理$AC=\sqrt{BC^{2}-AB^{2}}=\sqrt{10^{2}-6^{2}} = 8$。
2. 求$BD$、$CD$的长:
因为$AD$平分$\angle CAB$,所以$\angle CAD=\angle BAD$,则$CD = BD$。
在$Rt\triangle BCD$中,$BC = 10$,根据勾股定理$BD^{2}+CD^{2}=BC^{2}$,又$CD = BD$,所以$2BD^{2}=100$,解得$BD = CD = 5\sqrt{2}$。
(2)
连接$OB$、$OD$,因为$AD$平分$\angle CAB$,$\angle CAB = 60^{\circ}$,所以$\angle DAB=\frac{1}{2}\angle CAB = 30^{\circ}$。
根据同弧所对的圆心角是圆周角的$2$倍,$\angle BOD = 2\angle BAD=60^{\circ}$。
又因为$OB = OD$,所以$\triangle BOD$是等边三角形。
已知$\odot O$的直径为$10$,则半径$OB = 5$,所以$BD = OB = 5$。
综上,(1)中$AC = 8$,$BD = 5\sqrt{2}$,$CD = 5\sqrt{2}$;(2)中$BD$的长为$5$。
1. 若$AB是半径为5cm的\odot O$中的一条弦,且$AB = 8cm$,则$\odot O上到AB距离为3cm$的点有
2
个.答案:2
解析:
过圆心O作AB的垂线,垂足为M,连接OA。由垂径定理得AM=AB/2=4cm。在Rt△OAM中,OA=5cm,AM=4cm,由勾股定理得OM=√(OA²-AM²)=√(5²-4²)=3cm,即圆心O到AB的距离为3cm。
到AB距离为3cm的点的轨迹是两条平行于AB的直线l₁、l₂(AB两侧各一条)。
直线l₁与AB在圆心O同侧,圆心O到l₁的距离为|OM - 3|=0cm(即l₁过圆心),故l₁与⊙O交于2点;
直线l₂与AB在圆心O异侧,圆心O到l₂的距离为OM + 3=6cm,因6>5(半径),故l₂与⊙O无交点。
综上,⊙O上到AB距离为3cm的点有2个。
到AB距离为3cm的点的轨迹是两条平行于AB的直线l₁、l₂(AB两侧各一条)。
直线l₁与AB在圆心O同侧,圆心O到l₁的距离为|OM - 3|=0cm(即l₁过圆心),故l₁与⊙O交于2点;
直线l₂与AB在圆心O异侧,圆心O到l₂的距离为OM + 3=6cm,因6>5(半径),故l₂与⊙O无交点。
综上,⊙O上到AB距离为3cm的点有2个。
2. 如图,$PA$、$PB都是\odot O$的切线,切点分别为$A$、$B$,$\angle APB = 60^{\circ}$,$\odot O的半径是3cm$,则$\angle AOB = $
120°
,$PA = $3√3cm
.答案:120°,3√3cm
解析:
∵PA、PB是⊙O的切线,∴OA⊥PA,OB⊥PB,∴∠OAP=∠OBP=90°。在四边形OAPB中,∠AOB=360°-∠OAP-∠OBP-∠APB=360°-90°-90°-60°=120°。
连接OP,∵PA、PB是⊙O的切线,∴OP平分∠APB,PA=PB,∴∠APO=∠APB/2=30°。在Rt△OAP中,OA=3cm,∠APO=30°,∴OP=2OA=6cm,PA=√(OP²-OA²)=√(6²-3²)=3√3cm。
连接OP,∵PA、PB是⊙O的切线,∴OP平分∠APB,PA=PB,∴∠APO=∠APB/2=30°。在Rt△OAP中,OA=3cm,∠APO=30°,∴OP=2OA=6cm,PA=√(OP²-OA²)=√(6²-3²)=3√3cm。
3. 已知一个扇形的半径为$60cm$,圆心角为$150^{\circ}$,用它围成一个圆锥的侧面,则圆锥的底面圆半径为
25
$cm$.答案:$25$
解析:
本题可先根据扇形的弧长公式求出扇形的弧长,再根据圆锥底面圆周长等于扇形弧长来计算圆锥底面圆半径。
步骤一:计算扇形的弧长
扇形的弧长公式为$l = \frac{n\pi r}{180}$(其中$l$为弧长,$n$为圆心角度数,$r$为扇形半径)。
已知扇形半径$r = 60cm$,圆心角$n = 150^{\circ}$,将其代入公式可得:
$l=\frac{150×\pi×60}{180}=50\pi(cm)$
步骤二:计算圆锥的底面圆半径
设圆锥底面圆半径为$R$,因为圆锥底面圆的周长等于扇形的弧长,而圆的周长公式为$C = 2\pi R$(其中$C$为周长,$R$为半径),所以可得$2\pi R = 50\pi$,两边同时除以$2\pi$,解得$R = 25(cm)$。
步骤一:计算扇形的弧长
扇形的弧长公式为$l = \frac{n\pi r}{180}$(其中$l$为弧长,$n$为圆心角度数,$r$为扇形半径)。
已知扇形半径$r = 60cm$,圆心角$n = 150^{\circ}$,将其代入公式可得:
$l=\frac{150×\pi×60}{180}=50\pi(cm)$
步骤二:计算圆锥的底面圆半径
设圆锥底面圆半径为$R$,因为圆锥底面圆的周长等于扇形的弧长,而圆的周长公式为$C = 2\pi R$(其中$C$为周长,$R$为半径),所以可得$2\pi R = 50\pi$,两边同时除以$2\pi$,解得$R = 25(cm)$。