3. 已知$\odot O的直径为10cm$,弦$AB的长为6cm$,以点$O为圆心画一个小圆与AB$相切,则小圆的半径是(
A.$3cm$
B.$4cm$
C.$5cm$
D.$6cm$
B
)A.$3cm$
B.$4cm$
C.$5cm$
D.$6cm$
答案:B
解析:
过点O作OC⊥AB于点C,连接OA。
∵AB=6cm,∴AC=BC=3cm。
∵⊙O直径为10cm,∴OA=5cm。
在Rt△OAC中,OC=√(OA²-AC²)=√(5²-3²)=4cm。
∵小圆与AB相切,∴小圆半径为OC=4cm。
∵AB=6cm,∴AC=BC=3cm。
∵⊙O直径为10cm,∴OA=5cm。
在Rt△OAC中,OC=√(OA²-AC²)=√(5²-3²)=4cm。
∵小圆与AB相切,∴小圆半径为OC=4cm。
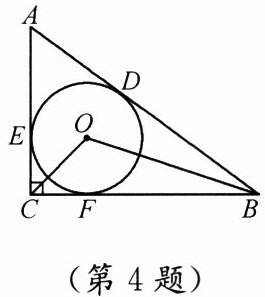
4. 如图,$\odot O是Rt\triangle ABC$的内切圆,切点分别为$D$、$E$、$F$,$\angle ACB = 90^{\circ}$,$\angle BOC = 115^{\circ}$,则$\angle ABC = $
40°
.
答案:40°
解析:
∵⊙O是Rt△ABC的内切圆,∴点O是△ABC的内心,BO平分∠ABC,CO平分∠ACB.
∵∠ACB=90°,∴∠OCB=∠ACB/2=45°.
在△BOC中,∠BOC=115°,∠OCB=45°,
∴∠OBC=180°-∠BOC-∠OCB=180°-115°-45°=20°.
∵BO平分∠ABC,∴∠ABC=2∠OBC=2×20°=40°.
∵∠ACB=90°,∴∠OCB=∠ACB/2=45°.
在△BOC中,∠BOC=115°,∠OCB=45°,
∴∠OBC=180°-∠BOC-∠OCB=180°-115°-45°=20°.
∵BO平分∠ABC,∴∠ABC=2∠OBC=2×20°=40°.
5. 如图,在矩形$ABCD$中,$AB = 2$,$BC = 3$,以点$A$为圆心,以$1为半径画\odot A$,$E是\odot A$上一动点,$P是BC$上一动点,则$PE + PD$的最小值为______

4
.
答案:4
解析:
以BC为对称轴作点A的对称点A',连接A'D交BC于点P,此时PA+PD最小,最小值为A'D的长。
矩形ABCD中,AB=2,BC=3,∴A'(4,0),D(0,3)。
由勾股定理得A'D=√[(4-0)²+(0-3)²]=5。
∵E是⊙A上动点,PE最小值为PA-AE=PA-1,
∴PE+PD最小值为(PA+PD)-1=5-1=4。
矩形ABCD中,AB=2,BC=3,∴A'(4,0),D(0,3)。
由勾股定理得A'D=√[(4-0)²+(0-3)²]=5。
∵E是⊙A上动点,PE最小值为PA-AE=PA-1,
∴PE+PD最小值为(PA+PD)-1=5-1=4。
6. 如图,点$D在\odot O的直径AB$的延长线上,点$C在\odot O$上,$AC = CD$,$\angle ACD = 120^{\circ}$.
(1) 求证:$CD是\odot O$的切线;
(2) 若$\odot O的半径为2$,求图中阴影部分的面积.

(1) 求证:$CD是\odot O$的切线;
(2) 若$\odot O的半径为2$,求图中阴影部分的面积.

答案:(1)
连接$OC$。
因为$AC = CD$,$\angle ACD = 120^{\circ}$,所以$\angle A=\angle D = 30^{\circ}$。
因为$OA = OC$,所以$\angle A=\angle ACO = 30^{\circ}$。
所以$\angle OCD=\angle ACD - \angle ACO=120^{\circ}- 30^{\circ}=90^{\circ}$,即$OC\perp CD$。
又因为$OC$是$\odot O$的半径,所以$CD$是$\odot O$的切线。
(2)
因为$\angle A = 30^{\circ}$,所以$\angle COB = 2\angle A=60^{\circ}$。
在$Rt\triangle OCD$中,$\angle D = 30^{\circ}$,$OC = 2$,则$OD = 2OC = 4$,$CD=\sqrt{OD^{2}-OC^{2}}=\sqrt{4^{2}-2^{2}}=2\sqrt{3}$。
$S_{\triangle OCD}=\frac{1}{2}× OC× CD=\frac{1}{2}×2×2\sqrt{3}=2\sqrt{3}$。
$S_{扇形OBC}=\frac{60\pi×2^{2}}{360}=\frac{2}{3}\pi$。
$S_{阴影}=S_{\triangle OCD}-S_{扇形OBC}=2\sqrt{3}-\frac{2}{3}\pi$。
综上,(1)证明过程如上述;(2)阴影部分面积为$2\sqrt{3}-\frac{2}{3}\pi$。
连接$OC$。
因为$AC = CD$,$\angle ACD = 120^{\circ}$,所以$\angle A=\angle D = 30^{\circ}$。
因为$OA = OC$,所以$\angle A=\angle ACO = 30^{\circ}$。
所以$\angle OCD=\angle ACD - \angle ACO=120^{\circ}- 30^{\circ}=90^{\circ}$,即$OC\perp CD$。
又因为$OC$是$\odot O$的半径,所以$CD$是$\odot O$的切线。
(2)
因为$\angle A = 30^{\circ}$,所以$\angle COB = 2\angle A=60^{\circ}$。
在$Rt\triangle OCD$中,$\angle D = 30^{\circ}$,$OC = 2$,则$OD = 2OC = 4$,$CD=\sqrt{OD^{2}-OC^{2}}=\sqrt{4^{2}-2^{2}}=2\sqrt{3}$。
$S_{\triangle OCD}=\frac{1}{2}× OC× CD=\frac{1}{2}×2×2\sqrt{3}=2\sqrt{3}$。
$S_{扇形OBC}=\frac{60\pi×2^{2}}{360}=\frac{2}{3}\pi$。
$S_{阴影}=S_{\triangle OCD}-S_{扇形OBC}=2\sqrt{3}-\frac{2}{3}\pi$。
综上,(1)证明过程如上述;(2)阴影部分面积为$2\sqrt{3}-\frac{2}{3}\pi$。
7. 如图,已知直线$PA交\odot O于A$、$B$两点,$AE是\odot O$的直径,$C为\odot O$上的一点,且$AC平分\angle PAE$,过点$C作CD\perp PA$,垂足为$D$.
(1) 求证:$CD为\odot O$的切线;
(2) 已知$DC + DA = 6$,$\odot O的直径为10$,求$AB$的长.

(1) 求证:$CD为\odot O$的切线;
(2) 已知$DC + DA = 6$,$\odot O的直径为10$,求$AB$的长.

答案:(1) 证明见上;(2) AB=6。
解析:
(1) 证明:连接OC。
∵AC平分∠PAE,∴∠PAC=∠CAE。
∵OA=OC,∴∠OCA=∠CAE。
∴∠PAC=∠OCA,∴OC//PA。
∵CD⊥PA,∴OC⊥CD。
∵OC是⊙O半径,∴CD为⊙O的切线。
(2) 设AD=x,则DC=6-x。过O作OF⊥AB于F,∴AF=FB。
∵CD是切线,OC⊥CD,CD⊥PA,OF⊥AB,∴四边形OCDF是矩形。
∴OF=CD=6-x,DF=OC=5(⊙O直径为10,半径OC=5)。
∴AF=DF-AD=5-x。
在Rt△OAF中,OA²=AF²+OF²,即5²=(5-x)²+(6-x)²。
展开得:25=25-10x+x²+36-12x+x²,化简得2x²-22x+36=0,即x²-11x+18=0。
解得x=2或x=9(x=9时DC=6-9=-3舍去)。
∴AD=2,AF=5-2=3,∴AB=2AF=6。
∵AC平分∠PAE,∴∠PAC=∠CAE。
∵OA=OC,∴∠OCA=∠CAE。
∴∠PAC=∠OCA,∴OC//PA。
∵CD⊥PA,∴OC⊥CD。
∵OC是⊙O半径,∴CD为⊙O的切线。
(2) 设AD=x,则DC=6-x。过O作OF⊥AB于F,∴AF=FB。
∵CD是切线,OC⊥CD,CD⊥PA,OF⊥AB,∴四边形OCDF是矩形。
∴OF=CD=6-x,DF=OC=5(⊙O直径为10,半径OC=5)。
∴AF=DF-AD=5-x。
在Rt△OAF中,OA²=AF²+OF²,即5²=(5-x)²+(6-x)²。
展开得:25=25-10x+x²+36-12x+x²,化简得2x²-22x+36=0,即x²-11x+18=0。
解得x=2或x=9(x=9时DC=6-9=-3舍去)。
∴AD=2,AF=5-2=3,∴AB=2AF=6。