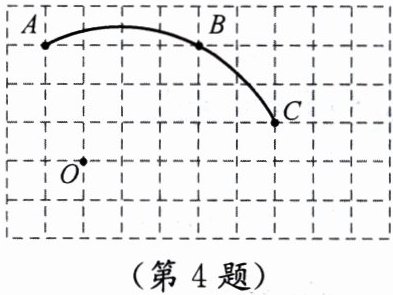
4.如图,在单位长度为1的正方形网格中,一段圆弧经过格点$A$、$B$、$C$.
(1)请完成如下操作:
①以$O$为原点、竖直和水平方向所在的直线为坐标轴、网格边长为单位长度,建立平面直角坐标系;
②确定该圆弧所在圆的圆心$D$,并连接$AD$、$CD$.
(2)请在(1)的基础上,完成下列问题:
①点$C$的坐标为
②$\odot D$的半径为
③若扇形$DAC$是一个圆锥的侧面展开图,则该圆锥的底面积为
④若点$E的坐标为(6,-1)$,试判断直线$CE与\odot D$的位置关系,并说明你的理由.
(第4题)
(1)请完成如下操作:
①以$O$为原点、竖直和水平方向所在的直线为坐标轴、网格边长为单位长度,建立平面直角坐标系;
②确定该圆弧所在圆的圆心$D$,并连接$AD$、$CD$.
(2)请在(1)的基础上,完成下列问题:
①点$C$的坐标为
(6,2)
,点$D$的坐标为(2,0)
;②$\odot D$的半径为
$2\sqrt{5}$
(结果保留根号);③若扇形$DAC$是一个圆锥的侧面展开图,则该圆锥的底面积为
$\frac{5}{4}\pi$
(结果保留$\pi$);④若点$E的坐标为(6,-1)$,试判断直线$CE与\odot D$的位置关系,并说明你的理由.
相交。理由:直线CE为x=6,圆心D(2,0)到直线x=6的距离为4,半径$2\sqrt{5}\approx4.47$,因为$4<2\sqrt{5}$,所以直线CE与$\odot D$相交。
(第4题)

答案:(1)①建立平面直角坐标系如图所示(以O为原点,水平向右为x轴正方向,竖直向上为y轴正方向);②圆心D为线段AB、BC垂直平分线的交点,图略。
(2)①(6,2);(2,0)
②$2\sqrt{5}$
③$\frac{5}{4}\pi$
④相交。理由:直线CE为x=6,圆心D(2,0)到直线x=6的距离为4,半径$2\sqrt{5}\approx4.47$,因为$4<2\sqrt{5}$,所以直线CE与$\odot D$相交。
(2)①(6,2);(2,0)
②$2\sqrt{5}$
③$\frac{5}{4}\pi$
④相交。理由:直线CE为x=6,圆心D(2,0)到直线x=6的距离为4,半径$2\sqrt{5}\approx4.47$,因为$4<2\sqrt{5}$,所以直线CE与$\odot D$相交。
5.如图,$AB是\odot O$的直径,$BC = 2cm$,$\angle ABC = 60^{\circ}$.
(1)求$\odot O$的直径.
(2)若$D是AB$延长线上一点,连接$CD$,当$BD$长为多少时,$CD与\odot O$相切?
(3)若动点$E以2cm/s的速度从点A出发沿着AB$方向运动,同时动点$F以1cm/s的速度从点B出发沿BC$方向运动.设运动时间为$t(s)(0 < t < 2)$,连接$EF$,当$t$为何值时,$\triangle BEF$为直角三角形?
(第5题)

(1)求$\odot O$的直径.
(2)若$D是AB$延长线上一点,连接$CD$,当$BD$长为多少时,$CD与\odot O$相切?
(3)若动点$E以2cm/s的速度从点A出发沿着AB$方向运动,同时动点$F以1cm/s的速度从点B出发沿BC$方向运动.设运动时间为$t(s)(0 < t < 2)$,连接$EF$,当$t$为何值时,$\triangle BEF$为直角三角形?
(第5题)

答案:(1) 4cm;(2) 2cm;(3) t=1或t=8/5。
解析:
(1) ∵AB是⊙O直径,∴∠ACB=90°(直径所对圆周角是直角)。
在Rt△ABC中,∠ABC=60°,BC=2cm,
cos∠ABC=BC/AB,即cos60°=2/AB,
∵cos60°=1/2,∴1/2=2/AB,解得AB=4cm。
∴⊙O的直径为4cm。
(2) 连接OC,∵CD与⊙O相切,∴OC⊥CD(切线垂直于过切点的半径)。
∵OB=OC=2cm(半径),BC=2cm,∴△OBC为等边三角形,∠OCB=60°。
∴∠BCD=∠OCD-∠OCB=90°-60°=30°。
∵∠CBD=180°-∠ABC=120°(平角定义),
∴∠BDC=180°-∠CBD-∠BCD=30°,∴∠BDC=∠BCD,
∴BD=BC=2cm。
(3) 由题意得:AE=2t,BF=t,∴BE=AB-AE=4-2t(0<t<2)。
情况1:∠BEF=90°
在Rt△BEF中,cos∠EBF=BE/BF,∠EBF=60°,
∴cos60°=(4-2t)/t,即1/2=(4-2t)/t,
解得t=8/5。
情况2:∠BFE=90°
在Rt△BEF中,cos∠EBF=BF/BE,∠EBF=60°,
∴cos60°=t/(4-2t),即1/2=t/(4-2t),
解得t=1。
综上,t=1s或t=8/5s。
在Rt△ABC中,∠ABC=60°,BC=2cm,
cos∠ABC=BC/AB,即cos60°=2/AB,
∵cos60°=1/2,∴1/2=2/AB,解得AB=4cm。
∴⊙O的直径为4cm。
(2) 连接OC,∵CD与⊙O相切,∴OC⊥CD(切线垂直于过切点的半径)。
∵OB=OC=2cm(半径),BC=2cm,∴△OBC为等边三角形,∠OCB=60°。
∴∠BCD=∠OCD-∠OCB=90°-60°=30°。
∵∠CBD=180°-∠ABC=120°(平角定义),
∴∠BDC=180°-∠CBD-∠BCD=30°,∴∠BDC=∠BCD,
∴BD=BC=2cm。
(3) 由题意得:AE=2t,BF=t,∴BE=AB-AE=4-2t(0<t<2)。
情况1:∠BEF=90°
在Rt△BEF中,cos∠EBF=BE/BF,∠EBF=60°,
∴cos60°=(4-2t)/t,即1/2=(4-2t)/t,
解得t=8/5。
情况2:∠BFE=90°
在Rt△BEF中,cos∠EBF=BF/BE,∠EBF=60°,
∴cos60°=t/(4-2t),即1/2=t/(4-2t),
解得t=1。
综上,t=1s或t=8/5s。