1. 已知函数 $ y = 2x + 1 $ 的自变量 $ x $ 所取的值 $ x_1 $、$ x_2 $、$ x_3 $、$ x_4 $、$ x_5 $ 的平均数为 2,方差为 0.25,则对应的函数值 $ y_1 $、$ y_2 $、$ y_3 $、$ y_4 $、$ y_5 $ 的平均数为
5
,方差为1
。答案:5,1
解析:
已知$x$的平均数$\bar{x}=2$,方差$s_x^2=0.25$,函数$y=2x + 1$。
对于平均数:$\bar{y}=2\bar{x}+1=2×2 + 1=5$。
对于方差:$y_i - \bar{y}=2(x_i - \bar{x})$,则$s_y^2=2^2s_x^2=4×0.25=1$。
对于平均数:$\bar{y}=2\bar{x}+1=2×2 + 1=5$。
对于方差:$y_i - \bar{y}=2(x_i - \bar{x})$,则$s_y^2=2^2s_x^2=4×0.25=1$。
2. 某校倡议九年级学生利用双休日在社区参加义务劳动。为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并将得到的数据绘制成如下不完整的统计图表:
|劳动时间/h|频数(人数)|频率|
|0.5|12|0.12|
|1|30|0.3|
|1.5|x|0.4|
|2|18|y|
|合计|m|1|
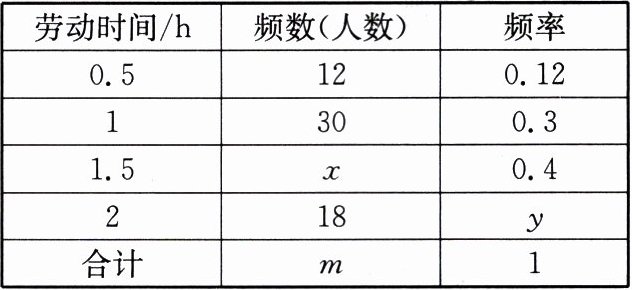

(1)统计表中的 $ m = $______,$ x = $______,$ y = $______;
(2)被调查同学劳动时间的中位数是______h;
(3)请将频数分布直方图补充完整;
(4)求所有被调查同学的平均劳动时间。
(1)
(2)
(3)在直方图中1.5h对应的长方形高画为40(此处为文字描述补充操作)
(4)
|劳动时间/h|频数(人数)|频率|
|0.5|12|0.12|
|1|30|0.3|
|1.5|x|0.4|
|2|18|y|
|合计|m|1|


(1)统计表中的 $ m = $______,$ x = $______,$ y = $______;
(2)被调查同学劳动时间的中位数是______h;
(3)请将频数分布直方图补充完整;
(4)求所有被调查同学的平均劳动时间。
(1)
100
40
0.18
(2)
1.5
(3)在直方图中1.5h对应的长方形高画为40(此处为文字描述补充操作)
(4)
$\frac{12×0.5 + 30×1 + 40×1.5 + 18×2}{100}=\frac{6 + 30 + 60 + 36}{100}=\frac{132}{100}=1.32(h)$,所以所有被调查同学的平均劳动时间为1.32h。
答案:(1)
$m = 12÷0.12 = 100$;
$x = 100×0.4 = 40$;
$y = 18÷100 = 0.18$;
故答案为:$100$;$40$;$0.18$。
(2)
将劳动时间从小到大排列,总人数为$100$人,中位数是第$50$、$51$个数的平均数,前两组共有$12 + 30 = 42$人,前三组共有$42 + 40 = 82$人,所以中位数在$1.5h$这一组,中位数是$1.5h$。
(3)
$1.5h$对应的频数为$40$,在直方图中$1.5h$对应的长方形高为$40$,补充直方图(此处无法实际画图,在$1.5$对应的位置画高度为$40$的长方形)。
(4)
$\frac{12×0.5 + 30×1 + 40×1.5 + 18×2}{100}$
$=\frac{6 + 30 + 60 + 36}{100}$
$=\frac{132}{100}= 1.32(h)$
所以所有被调查同学的平均劳动时间为$1.32h$。
$m = 12÷0.12 = 100$;
$x = 100×0.4 = 40$;
$y = 18÷100 = 0.18$;
故答案为:$100$;$40$;$0.18$。
(2)
将劳动时间从小到大排列,总人数为$100$人,中位数是第$50$、$51$个数的平均数,前两组共有$12 + 30 = 42$人,前三组共有$42 + 40 = 82$人,所以中位数在$1.5h$这一组,中位数是$1.5h$。
(3)
$1.5h$对应的频数为$40$,在直方图中$1.5h$对应的长方形高为$40$,补充直方图(此处无法实际画图,在$1.5$对应的位置画高度为$40$的长方形)。
(4)
$\frac{12×0.5 + 30×1 + 40×1.5 + 18×2}{100}$
$=\frac{6 + 30 + 60 + 36}{100}$
$=\frac{132}{100}= 1.32(h)$
所以所有被调查同学的平均劳动时间为$1.32h$。
3. 某中学为了解本校学生平均每天的课外学习时间情况,随机抽取部分学生进行问卷调查,并将调查结果分为 A、B、C、D 四个等级,设学习时间为 $ t $(h),A:$ t < 1 $,B:$ 1 \leqslant t < 1.5 $,C:$ 1.5 \leqslant t < 2 $,D:$ t \geqslant 2 $,根据调查结果绘制了如图所示的两幅不完整的统计图。请你根据图中信息解答下列问题:

(1)本次抽样调查共抽取了多少名学生?请将条形统计图补充完整。
(2)本次抽样调查中,学习时间的中位数落在哪个等级内?
(3)B 等级对应的扇形圆心角 $ \alpha $ 的度数是多少?

(1)本次抽样调查共抽取了多少名学生?请将条形统计图补充完整。
(2)本次抽样调查中,学习时间的中位数落在哪个等级内?
(3)B 等级对应的扇形圆心角 $ \alpha $ 的度数是多少?
答案:(1)200名,C等级人数40;(2)C等级;(3)$54^\circ$。
解析:
(1) 总人数:$60÷30\% = 200$(名)。
C等级人数:$200 - 60 - 30 - 70 = 40$(名),补充条形统计图C对应人数为40。
(2) 总人数200,中位数为第100和101个数据的平均数。
累计人数:A(60),B(60+30=90),C(90+40=130)。
第100和101个数据落在C等级,故中位数在C等级。
(3) B等级百分比:$\frac{30}{200}×100\% = 15\%$,
圆心角$\alpha = 15\%×360^\circ = 54^\circ$。
C等级人数:$200 - 60 - 30 - 70 = 40$(名),补充条形统计图C对应人数为40。
(2) 总人数200,中位数为第100和101个数据的平均数。
累计人数:A(60),B(60+30=90),C(90+40=130)。
第100和101个数据落在C等级,故中位数在C等级。
(3) B等级百分比:$\frac{30}{200}×100\% = 15\%$,
圆心角$\alpha = 15\%×360^\circ = 54^\circ$。