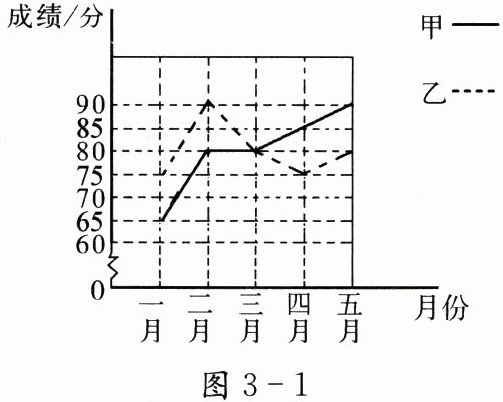
为了从甲、乙两人中选拔一人参加物理实验操作能力竞赛,每个月对他们的实验操作进行一次测验,如图 3 - 1 给出了两人赛前的 5 次测验成绩。
(1)分别求出甲、乙两人 5 次测验成绩的平均数和方差。
(2)你认为应该选派谁参加这次竞赛,有何建议?请结合图形简要说明理由。
(1)分别求出甲、乙两人 5 次测验成绩的平均数和方差。
(2)你认为应该选派谁参加这次竞赛,有何建议?请结合图形简要说明理由。

答案:(1)甲的成绩:65,80,80,85,90;乙的成绩:75,90,80,75,80。
甲的平均数:$\bar{x}_甲=\frac{65+80+80+85+90}{5}=80$
甲的方差:$S_甲^2=\frac{1}{5}[(65-80)^2+(80-80)^2+(80-80)^2+(85-80)^2+(90-80)^2]=\frac{1}{5}[225+0+0+25+100]=70$
乙的平均数:$\bar{x}_乙=\frac{75+90+80+75+80}{5}=80$
乙的方差:$S_乙^2=\frac{1}{5}[(75-80)^2+(90-80)^2+(80-80)^2+(75-80)^2+(80-80)^2]=\frac{1}{5}[25+100+0+25+0]=30$
(2)选派甲参加竞赛。理由:甲的成绩呈上升趋势,潜力较大。
甲的平均数:$\bar{x}_甲=\frac{65+80+80+85+90}{5}=80$
甲的方差:$S_甲^2=\frac{1}{5}[(65-80)^2+(80-80)^2+(80-80)^2+(85-80)^2+(90-80)^2]=\frac{1}{5}[225+0+0+25+100]=70$
乙的平均数:$\bar{x}_乙=\frac{75+90+80+75+80}{5}=80$
乙的方差:$S_乙^2=\frac{1}{5}[(75-80)^2+(90-80)^2+(80-80)^2+(75-80)^2+(80-80)^2]=\frac{1}{5}[25+100+0+25+0]=30$
(2)选派甲参加竞赛。理由:甲的成绩呈上升趋势,潜力较大。
1. 甲、乙两人在相同的条件下各打靶 10 次,经过计算:甲、乙射击成绩的平均数都是 8 环,甲成绩的方差是 1.2,乙成绩的方差是 1.8。下列说法中,不一定正确的是(
A.甲、乙射中的总环数相同
B.甲的成绩稳定
C.乙的成绩波动较大
D.甲、乙成绩的众数相同
D
)A.甲、乙射中的总环数相同
B.甲的成绩稳定
C.乙的成绩波动较大
D.甲、乙成绩的众数相同
答案:D
解析:
甲、乙射击成绩的平均数都是8环,各打靶10次,总环数都为8×10=80环,A正确;方差越小成绩越稳定,甲方差1.2<乙方差1.8,所以甲成绩稳定,乙成绩波动较大,B、C正确;平均数和方差与众数无关,无法确定众数是否相同,D不一定正确。
2. 学校开展为图书角捐书活动,以下是 5 名同学捐书的数量(单位:册):2,2,x,4,9。已知这组数据的平均数是 4,则这组数据的中位数和众数分别是
中位数是3,众数是2
。答案:中位数是$3$,众数是$2$(按照题目顺序填写答案对应内容)
解析:
根据平均数的定义,平均数等于所有数据之和除以数据的个数。
已知数据$2, 2, x, 4, 9$的平均数是$4$,数据个数为$5$,则$\frac{2 + 2 + x + 4 + 9}{5}=4$。
等式两边同时乘以$5$可得:$2 + 2 + x + 4 + 9 = 20$。
计算等式左边$2+2+4+9 = 17$,则$17 + x = 20$,解得$x = 3$。
将这组数据$2, 2, 3, 4, 9$按照从小到大的顺序排列后,中位数就是处于中间位置的数,这组数据有$5$个,中间的是第$3$个数据$3$,所以中位数是$3$。
众数是一组数据中出现次数最多的数据,在这组数据$2, 2, 3, 4, 9$中$2$出现的次数最多,所以众数是$2$。
已知数据$2, 2, x, 4, 9$的平均数是$4$,数据个数为$5$,则$\frac{2 + 2 + x + 4 + 9}{5}=4$。
等式两边同时乘以$5$可得:$2 + 2 + x + 4 + 9 = 20$。
计算等式左边$2+2+4+9 = 17$,则$17 + x = 20$,解得$x = 3$。
将这组数据$2, 2, 3, 4, 9$按照从小到大的顺序排列后,中位数就是处于中间位置的数,这组数据有$5$个,中间的是第$3$个数据$3$,所以中位数是$3$。
众数是一组数据中出现次数最多的数据,在这组数据$2, 2, 3, 4, 9$中$2$出现的次数最多,所以众数是$2$。
3. 某校对应聘者分别进行了教学能力、科研能力和组织能力三项测试,其中甲、乙两名应聘者上述各项的成绩分别为(单位:分)81、85、86,92、80、74。如果将教学能力、科研能力和组织能力三项测试得分按 5:3:2 的比例计算总成绩,那么______总成绩最高。
乙
答案:甲的总成绩为:
$\frac{81 × 5 + 85 × 3 + 86 × 2}{5 + 3 + 2}$
$ = \frac{405 + 255 + 172}{10}$
$ = \frac{832}{10}$
$ = 83.2$(分)
乙的总成绩为:
$\frac{92 × 5 + 80 × 3 + 74 × 2}{5 + 3 + 2}$
$ = \frac{460 + 240 + 148}{10}$
$ = \frac{848}{10}$
$ = 84.8$(分)
因为$84.8 \gt 83.2$,所以乙的总成绩最高。
故答案为乙。
$\frac{81 × 5 + 85 × 3 + 86 × 2}{5 + 3 + 2}$
$ = \frac{405 + 255 + 172}{10}$
$ = \frac{832}{10}$
$ = 83.2$(分)
乙的总成绩为:
$\frac{92 × 5 + 80 × 3 + 74 × 2}{5 + 3 + 2}$
$ = \frac{460 + 240 + 148}{10}$
$ = \frac{848}{10}$
$ = 84.8$(分)
因为$84.8 \gt 83.2$,所以乙的总成绩最高。
故答案为乙。