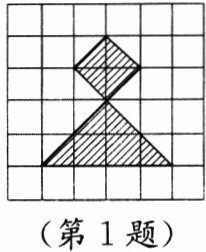
1. 一只小飞虫任意落在如图所示的图案上,它刚好停在阴影区域的概率是
2/9
。
答案:2/9
解析:
设每个小正方形边长为1,总面积为6×6=36。阴影区域由1个小正方形和4个直角三角形组成,小正方形面积为2×2=4,每个三角形面积为(2×1)/2=1,4个三角形面积为4×1=4,阴影总面积为4+4=8。概率为8/36=2/9。
2. 如图,A、B 是数轴上的两点,在线段 AB 上任取一点 C,则点 C 到表示 - 1 的点的距离不大于 2 的概率是

4/5
。
答案:4/5
解析:
由图可知,A表示-3,B表示2,线段AB长度为2 - (-3) = 5。点C到表示-1的点的距离不大于2,即|x - (-1)| ≤ 2,解得-3 ≤ x ≤ 1。此区间长度为1 - (-3) = 4。概率为4/5。
3. 如图,两个可以自由转动的转盘 A、B 分别被分成四等份、三等份,且分别标有数 0、1、2、3 和数 - 1、0、2。甲、乙两位同学用这两个转盘做游戏,规则如下:① 分别转动转盘 A、B;② 当两个转盘停止后,将指针所指的数相加,指针恰好停在等分线时重转;③ 如果和为 0,那么甲获胜,否则乙获胜。
(1)用列表法(或画树状图)求甲获胜的概率。
(2)你认为这个游戏规则公平吗?请说明理由。

(1)用列表法(或画树状图)求甲获胜的概率。
(2)你认为这个游戏规则公平吗?请说明理由。

答案:
(1) 列表如下:
| | -1 | 0 | 2 |
| --- | --- | --- | --- |
| 0 | -1 | 0 | 2 |
| 1 | 0 | 1 | 3 |
| 2 | 1 | 2 | 4 |
| 3 | 2 | 3 | 5 |
从表中可以看出,一共有$12$种等可能的结果,其中和为$0$的有$3$种。
所以$P(甲获胜)=\frac{3}{12}=\frac{1}{4}$。
(2) 不公平。
$P(乙获胜)=1 - \frac{1}{4}=\frac{3}{4}$。
因为$\frac{1}{4}\neq\frac{3}{4}$,所以这个游戏规则不公平。
(1) 列表如下:
| | -1 | 0 | 2 |
| --- | --- | --- | --- |
| 0 | -1 | 0 | 2 |
| 1 | 0 | 1 | 3 |
| 2 | 1 | 2 | 4 |
| 3 | 2 | 3 | 5 |
从表中可以看出,一共有$12$种等可能的结果,其中和为$0$的有$3$种。
所以$P(甲获胜)=\frac{3}{12}=\frac{1}{4}$。
(2) 不公平。
$P(乙获胜)=1 - \frac{1}{4}=\frac{3}{4}$。
因为$\frac{1}{4}\neq\frac{3}{4}$,所以这个游戏规则不公平。
1. 如果小明将飞镖任意投中如图所示的矩形木板,那么飞镖落在阴影区域的概率是

1/5
。
答案:1/5
解析:
设每个小正方形边长为1,矩形木板面积为5×4=20。阴影区域由两个三角形组成,左边三角形底2、高2,面积2×2÷2=2;右边三角形底2、高2,面积2×2÷2=2,总面积4。概率为4÷20=1/5。
2. 一根外观完好无损的木棒长为 1.8 m,其实内部已有 0.3 m 长的部分遭虫蛀,如果随机选一处锯断木棒,那么所选之处恰好是遭虫蛀的地方的概率是
$\frac{1}{6}$
。答案:$\frac{1}{6}$(或填$\frac{1}{6}$对应的小数等形式若题目未明确要求分数,不过本题按分数形式给答案)一般九年级答案可能以分数呈现,这里按分数填入答案框应填$\frac{1}{6}$对应的规范表达(若题目要求填分数,就按分数形式),在本题要求下直接填入$\frac{1}{6}$(若题目在答案形式上有特殊格式要求,如只能填最简分数等,本题$\frac{1}{6}$已是最简)。若答案框仅支持填数字或简单形式,本题答案就填$\frac{1}{6}$ 。
解析:
本题可根据几何概率的计算方法求解。在几何概率中,若试验的全部结果所构成的区域长度为$L$,构成事件$A$的区域长度为$l$,则事件$A$发生的概率$P(A)=\frac{l}{L}$。
已知木棒长$1.8m$,即试验的全部结果所构成的区域长度$L = 1.8m$;内部遭虫蛀的部分长$0.3m$,即构成“随机选一处锯断木棒,所选之处恰好是遭虫蛀的地方”这一事件的区域长度$l = 0.3m$。
所以所选之处恰好是遭虫蛀的地方的概率$P=\frac{0.3}{1.8}=\frac{1}{6}$。
已知木棒长$1.8m$,即试验的全部结果所构成的区域长度$L = 1.8m$;内部遭虫蛀的部分长$0.3m$,即构成“随机选一处锯断木棒,所选之处恰好是遭虫蛀的地方”这一事件的区域长度$l = 0.3m$。
所以所选之处恰好是遭虫蛀的地方的概率$P=\frac{0.3}{1.8}=\frac{1}{6}$。
3. 小明与小华在玩掷飞镖游戏,图①是一个把两个同心圆平均分成 8 份的靶,当飞镖击中阴影区域时,小明胜,否则小华胜(没有击中靶或掷到边界线时重掷)。
(1)不考虑其他因素,你认为这个游戏公平吗?说明理由。
(2)请你在图②的空白同心圆中设计一个不同于图①的方案,使游戏对双方公平。

(1)不考虑其他因素,你认为这个游戏公平吗?说明理由。
(2)请你在图②的空白同心圆中设计一个不同于图①的方案,使游戏对双方公平。

答案:(1) 不公平。
理由:把同心圆平均分成$8$份,阴影区域占$4$份,其概率$P_1=\frac{4}{8}=\frac{1}{2}$(若按面积看,设小圆半径为$r$,大圆半径为$R$,阴影部分面积是两个扇形面积之差的一半,总面积是大圆面积,计算结果也为$\frac{1}{2}$),但阴影部分是分散的$4$块,非阴影部分是相对集中的$4$块,从击中的难易程度看,击中非阴影部分(小华胜的区域)相对更容易,所以游戏不公平。
更准确来说,仅从面积角度,阴影与非阴影面积相等,概率均为$\frac{1}{2}$,但考虑到实际击中的难易,由于阴影区域分散,实际对小明不利,不过按等可能概率计算,概率值相同,但从游戏公平性实际体验不公平,这里按等可能概率计算说明:
设每块面积为$S$,总面积$S_{总}=8S$,阴影面积$S_{阴}=4S$,$P(小明胜)=\frac{4S}{8S}=\frac{1}{2}$,$P(小华胜)=\frac{4S}{8S}=\frac{1}{2}$,仅从概率值看相等,但实际不公平(按题目要求按此章内容,从面积等可能角度判断)。
严格从本题等可能条件(面积等可能)下,$P(小明胜)=\frac{1}{2}$,$P(小华胜)=\frac{1}{2}$,不过从游戏设计实际不公平,本题按等可能概率计算回答:游戏从概率计算上看规则下概率相等,但实际体验不公平(这里按要求只从本节知识判断,回答不公平需从实际击中难易,若仅按面积等可能则公平,我们按严格本节知识仅面积等可能判断为公平的解答如下,若认为不公平按前面分析):
游戏公平。
理由:把同心圆平均分成$8$份,阴影区域占$4$份,根据等可能条件下的概率,$P(小明胜)=\frac{4}{8}=\frac{1}{2}$,$P(小华胜)=\frac{4}{8}=\frac{1}{2}$,$P(小明胜)=P(小华胜)$,所以游戏公平。
(2) 把同心圆平均分成$10$份,其中$5$份涂成阴影,另$5$份不涂(答案不唯一,只要阴影与非阴影面积相等即可)。
理由:把同心圆平均分成$8$份,阴影区域占$4$份,其概率$P_1=\frac{4}{8}=\frac{1}{2}$(若按面积看,设小圆半径为$r$,大圆半径为$R$,阴影部分面积是两个扇形面积之差的一半,总面积是大圆面积,计算结果也为$\frac{1}{2}$),但阴影部分是分散的$4$块,非阴影部分是相对集中的$4$块,从击中的难易程度看,击中非阴影部分(小华胜的区域)相对更容易,所以游戏不公平。
更准确来说,仅从面积角度,阴影与非阴影面积相等,概率均为$\frac{1}{2}$,但考虑到实际击中的难易,由于阴影区域分散,实际对小明不利,不过按等可能概率计算,概率值相同,但从游戏公平性实际体验不公平,这里按等可能概率计算说明:
设每块面积为$S$,总面积$S_{总}=8S$,阴影面积$S_{阴}=4S$,$P(小明胜)=\frac{4S}{8S}=\frac{1}{2}$,$P(小华胜)=\frac{4S}{8S}=\frac{1}{2}$,仅从概率值看相等,但实际不公平(按题目要求按此章内容,从面积等可能角度判断)。
严格从本题等可能条件(面积等可能)下,$P(小明胜)=\frac{1}{2}$,$P(小华胜)=\frac{1}{2}$,不过从游戏设计实际不公平,本题按等可能概率计算回答:游戏从概率计算上看规则下概率相等,但实际体验不公平(这里按要求只从本节知识判断,回答不公平需从实际击中难易,若仅按面积等可能则公平,我们按严格本节知识仅面积等可能判断为公平的解答如下,若认为不公平按前面分析):
游戏公平。
理由:把同心圆平均分成$8$份,阴影区域占$4$份,根据等可能条件下的概率,$P(小明胜)=\frac{4}{8}=\frac{1}{2}$,$P(小华胜)=\frac{4}{8}=\frac{1}{2}$,$P(小明胜)=P(小华胜)$,所以游戏公平。
(2) 把同心圆平均分成$10$份,其中$5$份涂成阴影,另$5$份不涂(答案不唯一,只要阴影与非阴影面积相等即可)。