4. 把代数式$3x^{3}-12x^{2}+12x$分解因式,结果正确的是(
A.$3x(x^{2}-4x+4)$
B.$3x(x-4)^{2}$
C.$3x(x+2)(x-2)$
D.$3x(x-2)^{2}$
D
)A.$3x(x^{2}-4x+4)$
B.$3x(x-4)^{2}$
C.$3x(x+2)(x-2)$
D.$3x(x-2)^{2}$
答案:D
解析:
$3x^{3}-12x^{2}+12x$
$=3x(x^{2}-4x+4)$
$=3x(x-2)^{2}$
D
$=3x(x^{2}-4x+4)$
$=3x(x-2)^{2}$
D
5. 把多项式$ax^{2}+2a^{2}x+a^{3}$分解因式的结果是
a(x+a)²
。答案:a(x+a)²
解析:
$ax^{2}+2a^{2}x+a^{3}=a(x^{2}+2ax+a^{2})=a(x+a)^{2}$
6. 如图是用四张全等的矩形纸片拼成的图形,请利用图中空白部分的面积的不同表示方法写出一个关于$a,b$的恒等式:
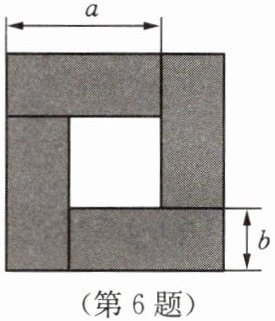
(a+b)²=(a-b)²+4ab
。
答案:(a+b)²=(a-b)²+4ab
解析:
$(a+b)^2=(a-b)^2+4ab$
7. 分解因式:
(1)$16a^{2}b^{2}c^{2}-9$;(2)$(x+y)^{2}-4(x+y)+4$;
(3)$(p-4)(p+1)+3p$;(4)$x-2xy+xy^{2}$;
(5)$(a^{2}+b^{2})^{2}-4a^{2}b^{2}$;(6)$9(x+2y)^{2}-4(x-y)^{2}$。
(1)$16a^{2}b^{2}c^{2}-9$;(2)$(x+y)^{2}-4(x+y)+4$;
(3)$(p-4)(p+1)+3p$;(4)$x-2xy+xy^{2}$;
(5)$(a^{2}+b^{2})^{2}-4a^{2}b^{2}$;(6)$9(x+2y)^{2}-4(x-y)^{2}$。
答案:(1)(4abc-3)(4abc+3);(2)(x+y-2)²;(3)(p+2)(p-2);(4)x(1-y)²;(5)(a+b)²(a-b)²;(6)(5x+4y)(x+8y)
解析:
(1)$16a^{2}b^{2}c^{2}-9=(4abc)^{2}-3^{2}=(4abc-3)(4abc+3)$;
(2)$(x+y)^{2}-4(x+y)+4=(x+y)^{2}-2×2×(x+y)+2^{2}=(x+y-2)^{2}$;
(3)$(p-4)(p+1)+3p=p^{2}+p-4p-4+3p=p^{2}-4=(p+2)(p-2)$;
(4)$x-2xy+xy^{2}=x(1-2y+y^{2})=x(1-y)^{2}$;
(5)$(a^{2}+b^{2})^{2}-4a^{2}b^{2}=(a^{2}+b^{2})^{2}-(2ab)^{2}=(a^{2}+b^{2}-2ab)(a^{2}+b^{2}+2ab)=(a-b)^{2}(a+b)^{2}$;
(6)$9(x+2y)^{2}-4(x-y)^{2}=[3(x+2y)]^{2}-[2(x-y)]^{2}=[3(x+2y)-2(x-y)][3(x+2y)+2(x-y)]=(3x+6y-2x+2y)(3x+6y+2x-2y)=(x+8y)(5x+4y)$。
8. 已知$x^{2}+y^{2}+4x-6y+13= 0$,求$x+y$的值。
答案:1
解析:
将原式变形为$(x^{2}+4x+4)+(y^{2}-6y+9)=0$,即$(x+2)^{2}+(y-3)^{2}=0$。
因为$(x+2)^{2}\geq0$,$(y-3)^{2}\geq0$,所以$x+2=0$,$y-3=0$,解得$x=-2$,$y=3$。
则$x+y=-2 + 3=1$。
1
因为$(x+2)^{2}\geq0$,$(y-3)^{2}\geq0$,所以$x+2=0$,$y-3=0$,解得$x=-2$,$y=3$。
则$x+y=-2 + 3=1$。
1